MATEMATYKA078

148 Ul. Rachunek różniczkowy

Oznacza to, że stosując wzór (4 3) dla f(x) = sinx wystarczy wybrać takie n, by

|R,(l)N^(sine + n|)|S^ <0,001.

Stąd wynika, źc można przyjąć n = 7. Zatem

“^nl*ir3! ⁺ 5!"⁰’⁸⁴¹⁷-    "

REGUŁA de LTIOSPITALA. Przy obliczaniu granic funkcji w przypadku symboli nieoznaczonych (por. rozdz. III, 1) korzystamy często z następującego twierdzenia nazywanego regułą de L'Hospitnln:

Jeżeli funkcje f i g są różniczkowalne na pewnym sąsiedztwie punktu x₀ oraz

1) limf(x) = 0    i limg(x) = 0,

X >x₀    X-»X*

f'(x)

2)    istnieje (właściwa lub niewłaściwa) granica lim —) ; ,

x-»x₀ g (x)

, przy czym f'(x)

f(x)

to istnieje również granica lim —)—£

x ►x_Mg(x)

lim

lim

f(x)

x~»x<,g(x) x-»x_a g^f(x)

Uwaga I. Sformułowane wyżej twierdzenie dotyczy obliczania granic wyrażeń typu Przy odpowiednio zmienionych założeniach, twierdzenie pozostaje prawdziwe w odniesieniu do symbolu

nieoznaczonego typu —, jak również dla granic jednostronnych (x x₀-

00

lub x -> x₀ + ) i granic w nieskończoności (x -* -oo lub x—>+00).

U w a g a 2. Twierdzenie odwrotne nic jest prawdziwe, o czym przekonuje nas przykład. Niech f(x) = x² sin—, g(x) = x. Wówczas:

X

Natomiast

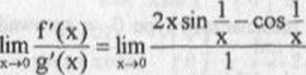
nic istnieje, gdyż nic istnieje lim cos—

*JV,    IMS* UUIIVjV lilii WJ

x *0 x

PRZY KŁAD 4.7 Obliczymy granice:

Obliczamy granicę ilorazu pochodnych: hm = lim 2x² = 2.

X—* 1 i    X—>1

X

Z reguły de L'Hospitala wynika, że istnieje również granica ilorazu funkcji, przy czym granice te są sobie równe:

W dalszym ciągu stosując regułę dc L'Hospitala będziemy pisać znak równości między granicą ilorazu funkcji i granicą ilorazu pochodnych, zanim o istnieniu tej drugiej granicy się przekonamy. Pamiętać jedynie należy, że w przypadku gdy okaże się, że granica ilorazu pochodnych nie istnieje, nie wolno nam wnioskować, żc nie istnieje granica ilorazu funkcji (por. uwaga 2).

1

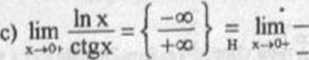
= lim MX(__sinx) = 10 = 0.

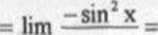
*-<K X

sin x

-lim®*

X -»04 X