MATEMATYKA087

166 Ul. Rachunek różniczkowy

WARUNEK WYSTARCZAJĄCY WYPUKŁOŚCI (WKLĘ-SIOŚCI) KRZYWEJ Wiemy już, że znak pierwszej pochodnej funkcji informuje nas o monotoniczności tej funkcji. Natomiast znak drugiej pochodnej pozwala nam, zgodnie z poniższym twierdzeniem, wnioskować o wypukłości lub wklęsłości wykresu danej funkcji.

TWIERDZENIE 6 I (warunek wystarczający wypukłości krzywej). Jeżeli funkcja f jest dwukrotnie różniczkowalna na przedziale (a,b), przy czym f"(x) > 0 dla każdego x z tego przedziału, lo krzywa y - f(x) jest wypukła na przedziale (a,b).

Dowód. Niech x₀ będzie dowolnie ustalonym punktem przedziału (a,b). Niech x będzie również dowolnym, ale różnym od x₀ punktem tego przedziału. Wówczas z twierdzenia Taylora (przy n - 2) wynika, że istnieje taki punkt c. pośredni między x i x₀, że

f(⁵‘) = f(x₀) + i^^<!)(x-x₀) + ^_!^c^(x x₀)^J.

Ponieważ

f"(c) > 0, gdyż c e(a,b) oraz (x - x₀)⁷ > 0, gdyż x * x₀, więc    f(x) - f(x₀) -f'(x₀)(x - Xo) = ~f"(c)(x -x₀)² > 0.

Stąd

f(x)>f(x₀) + f'(x₀)(x-x₀) dla x €(a*b)-{x₀}

Oznacza to, że krzywa y - f(x) jest wypukła w punkcie x₀, co wobec domyślności punktu x₀ €-(a,b) kończy dowód

TWIERDZENIE 6.2 (warunek wystarczający wklęsłości krzywej). Jeżeli funkcja fjcsł dwukrotnie różniczkowalna na przedziale (a,b), przy czym f"(x) < 0 dla każdego x z tego przedziału, to krzywa y - f(x) jest wklęsła na przedziale (a,b).

PUNKT PRZEGIĘCIA KRZYWEJ Punkt P₀(x₀,f(x₀)) nasuwamy punktem przegięcia krzywej y = f(x), gdy

1) istnieje styczna do tej krzywej w punkcie P₀ ( w szczególności może ta styczna być prostopadła do osi 0x)

oraz

2) krzywa la jest wypukła (wklęsła) na pewnym lewostronnym i wklęsła (wypukła) na pewnym prawostronnym sąsiedztwie punktu x₀.

W przypadku gdy ł*₀(x₀.f(x_ft)) jest punktem przegięciu krzywej y-f(x), mówmy też krócej, te krzywa ta ma w punkcie x₀ punkt przegięcia

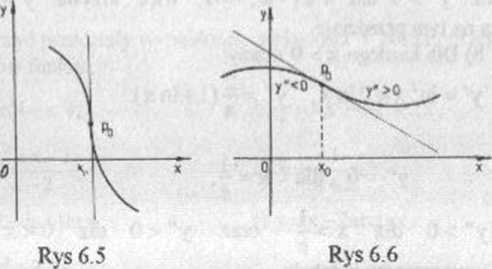
Na rysunkach 6.4 - 6.6 pokazane są krzywe, które mają punki przegięcia w punkcie x₀.

Z powyższych określeń i Iwicrdzeń 6.1 i 6.2 wynikają łatwo następujące twierdzenia:

TWIERDZENIE 6.3 (warunek konieczny istnienia punktu przegięcia). Jeżeli funkcja f ma ciągłą pochodną drugiego rzędu w punkcie x₀ i x₀ jest punktem przegięcia wykresu tej funkcji, to f"(x₀) = 0.

Jednocześnie należy pamiętać, że krzywa y = f(x) może mieć w x₀ punkt przegięcia nawet wtedy, gdy funkcja f nic jest różniczkowalna w tym punkcie (rys 6.5).

TWIERDZENIE 6.4 (warunek wystarczający istnienia punktu przegięcia). Jeżeli funkcja f jest dwukrotnie różniczkowalna na otoczeniu CJ(x₀,e) punktu x₀ oraz

(1)    f"(x)>0 dla x€(x_o-e,x₀) i f"(x)<0 dla xe(x₀,x₀+e) lub

(2)    f"(x)<0 dla xe(x₀-e,x₀) i f"(x)>0dla x€(x₀,x_o+e). to x₀ jest punktem przegięcia krzywej y = f(x).