MATEMATYKA065

122 Ul. Rachunek różniczkowy

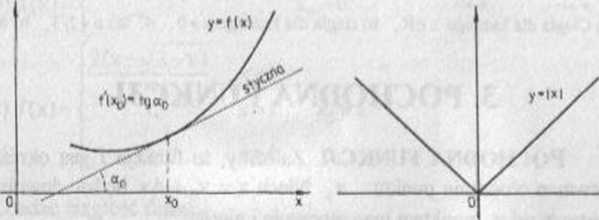
Przypomnijmy, źc pochodna f'(x₀) jest równa współczynnikowi kierunkowemu stycznej do wy kresu funkcji f poprowadzonej w punkcie

Rys 3.2

Rys 3.1

o odciętej x₀ (rys 3.1). W konsekwencji równanie stycznej do krzywej y = f(x) w punkcie (x₀,f(x₀)) ma postać

y-f(Xo) = ^f'(x₀)(*-X(,)

Uwaga Je?eli iloraz różnicowy J(x) funkcji f ma w- punkcie granicy niewłaściwą +co(-co)przyjmuje się czasem. że funkcja f ma w punkcie x₀ pochodną niewłaściwą (nieskończoną) równą +cc (-«>). Czytelnikowi pozostawiamy sprawdzenie. Ze funkcju

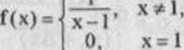
ma w punkcie X* « l pochodną niewłaściwą: f'(l) ■ +oo Zauważmy jednocześnie. Ze funkcja f nie jest ciągła w punkcie x₀ ■ I.

Jeżeli funkcja f jest ciągła w punkcie x₀ i ma w lym punkcie pochodną niewłaściwą -foo lul> -oo, to istnieje styczna do wykresu funkcji f w punkcie P₉(X0,f(Xg)) i jest ona prostopadła do osi 0x. a punkt P₀ jest punktem przegięcia wykresu tej funkcji (por paragraf 6 tego rozdziału).

W lej książce pochodna funkcji w punkcie oznaczać będzie zawsze, zgodnie z przyjętą wcześniej definicją, skończoną granicę ilorazu różnicowego. W innym przypadku mówić będziemy, żc pochodna nie istnieje.

PRZYKŁAD 3.1

a) Łatwo pokazać, żc funkcja f(x) =|x| (rys 3.2) ma pochodną w^f każdym punkcjc x *■ 0, przy czym

f'(x) =

-1, gdy x <0,

[1, gdy x > 0.

Wykażemy, żc funkcja f w punkcie x = 0 pochodnej nic ma. Iloraz różnicowy ma postać:

_J(x)=f&-f(Q)₌H

^v '    x-0 x

Ponieważ

^ = lim (-1) = -

X x-»0-

lim J(x) = lim ^ = lim ! = 1,

lim J(x) = lim ^ = lim (-1) = -1,

x-*0-    x >0 X x-»0-

x-»0+    x-»0» X x-»0»

więc lim J(x) nic istnieje, a zatem i pochodna funkcji f w punkcie x₀ = 0

x--*0

nic istnieje.

b) Obliczamy pochodną funkcji

f(x) =

l-x², gdy x£l,

lx²-4x + 3, gdy x>l w punkcie x₀ = 1.

Ponieważ funkcja jest określona różnymi wzorami w lewo- i prawostronnym sąsiedztwie punktu x₀ = 1, więc liczymy granice jednostronne ilorazu różnicowego:

X—*1-

x-*l-

lim £(^x)-|X’) ₌ lim 1^*1 = lim (-1- x) = -2,

X “ 1    x *1- X — 1

hm    = |im -^;~^4x-³= lim (x — 3) = —2.

X-*l» X — I    K-»l« X — 1    *-*l«

Stąd wynika, żc

X-*I X -1

Zatem pochodna funkcji f w punkcie x = 1 istnieje i f'(l) = -2. Czytelnikowi pozostawiamy naszkicowanie wykresu tej funkcji.