236 (51)

236

9. Ruch złożony punktu

Zadanie 9.1 o

i_WXl = jci = —r(o cos <ot _v2

ROZWIĄZANIE

Przy obliczeniu przyspieszenia bezwzględnego Skorzy! ze wzoru (9.7). Składowe przyspieszenia względnego wS* dzie ruchomym są równe    -a_wyi = yi = —rco sm <ot

Przyspieszenie unoszenia w tym przypadku jest równe a_u = o> x (co x />) = —pco² Składowe tego przyspieszenia

a_UXl = -co²r(\ + cos orf)

== —cor sm a>t

Przyspieszenie Coriolisa

0	0	—CO
-*1	y\	0	= 2<wyii
i	j	k
	CLcx\	= 2co^2r cos cot
	^acy\	= 2xo^2r sin cuf

Składowe przyspieszenia bezwzględnego będą więc równe

Qbx\ ⁼ &wz\ "k &uxi “k ®cx| —    ® ?

CLby\ ~ fliuzj “ł" CLuyi “1“ flcyi ⁼ 0

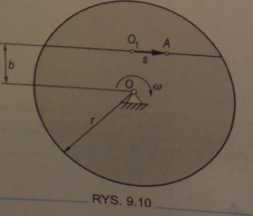
Koło o promieniu r obraca się wokół osi O ze stałą prędkością kątową co. Po cięciwie koła odległej od środka o odcinek b porusza się punkt A, którego współrzędna s — csinwl (c = y/r¹ — b²). Znaleźć prędkość bezwzględną i przyspieszenie bezwzględne punktu A (rys. 9.10).

Odpowiedź

Vb = (OyJb² + c² + 2bc cos cot ab = 2n>²v1 c² + bc cos eo*