Ruch złożony, prędkość

I

Ruch złożony punktu

Ruch złożony punktu

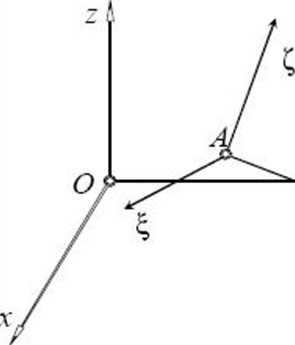
Rozpatrzmy punkt P poruszający się P    względem pewnego

układu odniesienia

który to układ porusza się ^    względem

X]    innego układu

odmesiema

Oxyz

Wielkości kinematy czne to wielkości występujące w kinematyce: tor. prędkość, pszyspieszenie. droga.

Wielkości kinematyczne bezwzględne to wielkości kinematyczne dotyczące poruszającego się punktu P odniesione do stałego układu odniesienia.

Wielkości kinematyczne względne to wielkości kinematyczne dotyczące poruszającego się punktu P odniesione do ruchomego układu odniesienia

Wielkości kinematyczne unoszenia to wielkości kinematyczne pizynależne temu punktowi mchomegc układu odniesienia, który w danej chwili pokrywa się z punktem P.

Inaczej mówiąc są to wielkości opisujące ruch układu ruchomego względem nieruchomego.

4

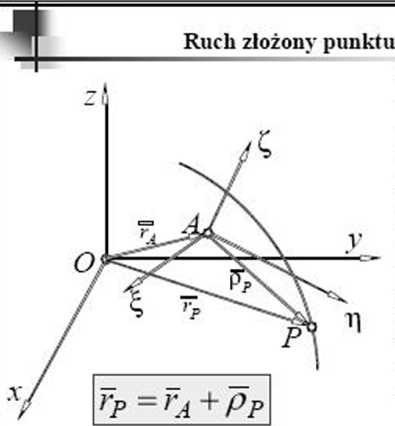
Ruch punktu P w układzie stałym nazwiemy ruchem bezwzględnym.

Ruch punktu P w ruchomym układzie ruchomym nazwiemy ruchem względnym.

Ruch układu ruchomego względem układu stałego nazwiemy ruchem unoszenia.

Prędkość w ruchu złożonym punktu

~P=~4+PP

Prędkość punktu wyrażamy jako pochodną promienia wektora

^rP = ^rA+pp

Uwzględniając reguły różniczkowania wektorów otrzymamy

« <fPp —    _ —

fp = ■    " + 7'^ + (O Xpp

ot