246 (40)

to do znacznego zwiększenia indukcyjności rozproszenia transformatora. Indukcyj-ność rozproszenia w tym przypadku oblicza się w następujący sposób:

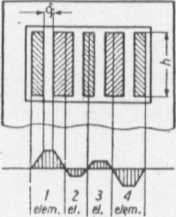
Z rys. XV. 33 widać, że wykres pola rozproszenia nie składa się już z jednako* wych elementów jak w przypadku uzwojenia symetrycznego; dlatego też uzwgjenie takie nazywa s^:ę niesymetryczne.

Dla wyznaczenia indukcyjności rozproszenia jednego elementu, których liczba jest — jak przedtem — mniejsza o jedność od liezby sekcji, obliczymy liczbę zwojów części pierwotnego uzwojenia transformatora przypadającej na dany element oraz grubość warstwy uzwojenia należącej do tego elementu zakładając, że gęstość zwojów jest równomierna oraz że liczby zwojów uzwojeń pierwotnego » wtórnego są jednakowe i równe 2. Przyjmiemy, że skrajne sekcje należą do uzwojenia pierwotnego; wtedy liczba zwojów każdego uzwojenia w pierwszym elemencie wyniesie

m + 2

(XV.58)

Rys. XV.33. Niesymetryczne uzwojenia krążkowe i wykresy ich strumieni rozproszeń,a

grubość zaś warstwy każdego uzwojenia w pierwszym elemencie będzie równa

2 2

^flu — A_t

m + 2 *

* m + 2

(XV.59)

Ponieważ liczba zwojów i grubość drugiej sekcji wyniosą

2 2

(XV.60)

więc liczbę zwojów i grubość warstwy drugiego elementu otrzymamy jako różnicę danych wielkości drugiej sekcji i pierwszego elementu

2	2 4
—■ £ 9 m m	+ 2 m(m + 2)
2	2 4
^A* m ^A'	hi + 2 “ m(m + 2)
	4
A ~ A	^1 m (m f- 2)

(XV.61)

W taki sam 6posób znajdziemy dla następnych elementów

2 (m - 2)

²*    ² m (m -f 2j

.    2(m    2)

* m (m + 2) 2 (m — 2)

-

m (m + 2) 8

H 8

m(m -f 2) 8

^ł| m (m -f- 2)

2 (m -4)

m (m -f- 2)

2 (hi 4) *• m (m + 2)

(XV.62) (XV.63)

(XV.64) (XV.65) (XV.66) (XV.67) (XV.68) (XV.69) (XV.70) (XV.71)

_i 2 (m — 4) *’• ~^A> m(m-f 2)

(XV.72)

i tak dalej Ponieważ krzywa rozkładu strumienia rozproszenia jest symetryczna względem środka, przeto sumowanie indukcyjności rozproszenia należy rozciągnąć tylko na połowę elementów oraz wynik pomnożyć przez dwa. Biorąc to pod uwagę i podstawiając do wzoru (XV. 48) wartości danych dotyczących poszczególnych elementów, otrzymamy po zsumowaniu

Lrk

0.8 n Icu

10« /»

{[(*)'(■*

m + 2

>]

A_t -+■ A,

U ^4 V	L ^At + ^A*	^4 \\
l\"i(m -f 2) f	3	m(m + 2)
r/2o--m*;	f * i ^A* + ^A*	2(m — 2) \1
[^ro(m + 2)/ 1	[^t + 3	m(m + 2)
U ^8 V	lu ^Ai + ^A*	^8 W
[(m(m + 2)|	(*+ 3	m(rn + 2) jj

+

A_x -I- A_t

2 (m — 4)

m (m -f-

+

.....}

(XV.73)

Wzór (XV. 73) pozwala obliczyć indukcyjność rozproszenia niesymetrycznego uzwojenia krążkowego o liczbie sekcd do 11; przy liczbie sekcji mniejszej od 11 bierze się do rachunku nie wszystkie wyrazy występujące w nawiasach kwadratowych. Na przysiad przy siedmiu sekcjach jest szesć elementów, a indukcyjność rozproszenia oblicza się tylko dla trzech elementów, a więc oblicza się tylko pierwsze trzy wyrazy w nawiasach kwadratowych.

Obliczenia wykazują, że indukcyjność rozproszenia takiego uzwojenia w zależności od liczby sekcji i odległości między nimi jest 1,2 -r 1,5 raza większa od indukcyjności rozproszenia symetrycznego uzwojenia o tej samej liczbie sekcji.

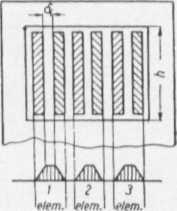
Przy parzystej liczbie sekcji uzwojeń cylindrycznych lub krążkowych i jednakowych sekcjach indukcyjność rozproszenia wzrasta jeszcze bardziej; dlatego też nie należy stosować parzystej liczby sekcji. Prócz tego przy parzystej liczbie sekcji uzwojenia nie mogą być symetrycznymi, jakimi niekiedy być muszą.

Rys. XV.34. Uzwojenia o parzystej liczbie sekcji i wykresy ich strumieni rozproszenia

Po wykreśleniu rozkładu strumienia rozproszenia (rys. XV. 34) przekonamy się, że omawiane nawinięcie dzieli się na jednakowe elementy, których liczba jest dwa razy mniejsza od liczby przeplatanych sekcji

(XV.74)

Liczby zwojów należących do poszczególnych elementów oraz grubość nawinięcia pojedynczego elementu w tym przypadku wynoszą

(XV.75)

h    24,    24,

Po podstawieniu danych jednego elementu do wzoru (XV. 48) i pomnożeniu wyniku przez liczbę elementów otrzymamy

^Lrk

4    0.4 7ik/_<Mj*

**    7u“ *

^s _1' ~ł~ ^A*

2 ⁺    "3

)

(XV.76)

Z porównania wzorów (XV 76) i (XV. 55) wynika, że przy liczbie przepleceń większej od pięciu przejście na ten typ nawijania przez zwiększenie liczby sekcji o jeden powoduje nie zmniejszenie, lecz zwiększenie indukcyjności rozproszenia transformatora, a stąd widać niecelowość stosowania parzystej liczby sekcji przeplatanych.