252 (9)

W obu tych przypadkach równania obserwacyjne dia kąta a_icp są identyczne i mają postać

^aLCł> - ^ACP ~ ^acl = ^kcp ^{+ C}c ~U<cl + C_c)~ K_a> - K_a =

Yp ~Y_C    Y, - Y_c

— arctg — —— arctg — -— —-

X p-X _c X_L-X_C

Na tej podstawie można sformułować następujące nieliniowe równanie poprawki:

»b

a,ri>+ l'„

Y_r

y_l~y_c

= arctg--------— arctg

X_P-X_C    X i - X _c

^lLCI> ^r va_LC!>

Natomiast jego liniowe pi'zybłiżenie można zapisać w postaci

da,_£J

dX, I ₀‘

da_lc/, I dX_c I „

^ IXł«x"

, ć)of,_a>! d_v +--—[    d.

o

, da d _v + —

_vo _vr> '“ ⁷c

dr„

0    y,!)

i. ~ ^rc

•ć * ^arc‘S -_x—~-_xT ~ ^arclg VŚ~T - «.

XI-Xc

^(,LCf

Wyznaczając odpowiednie pochodne, uzyskujemy

**tcp _    3

3^    3*,/ ^hX_L~X_c dl

CL

3«,o

dr,

3JT,

a y_l-y_c

—-r—arctg—---—•

ar,    x_L-x_c

d    Y,> - Y_c

-..........arctg —-----•— =

P dX_P    Xp - X_c

CT

3«lc/>

ar

d&LCP _— 3

ar,;

ar.

3^f*r.cy^> _ 3

d V_r    ” d r,

CL

&X,

CL

dr,

CL

Ar,

__CP

^dCP

arctg

-arctg

Yp “ Yc	_ *xa
X p~Xc	^dCP
. Yp - Yc	d
’xP-xc	d,rc
Yp - Yc	d
Xp~Xc	arc“

r, — r_c ay_c/> Ar,

arctg ——.....—— = —~-

X_L~X_C Ą_{p d}~

Yl-Y_C X_L-X_c

cl

i

ĆL

&x,

JCP , &Xcl

j²    .2

^dCP    ^dCL

Przykłady

Przykład 5.1.1

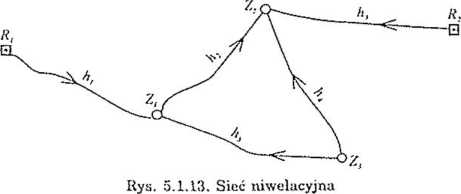
W sieci niwelacyjnej przedstawionej na rys. 5.1.13 zmierzono przewyższenia, uzyskując wyniki (w metrach):

hf =	2.371
hf =	4.768
hf =	-8.142
hf =	2.961
i ob h5 =	-1.774

Zatem

AY&

^V’^aiC/J (^)^yP '^Y/- (4J

____________________________,

^cz.)

^x W- '

.f Ą& ^A1s 1,

1 KV>' «_Ł)²j

r;v i , f ax9-_P    ax£, i _n

__ A-yo

,CP ^a LCP

*^uLCP

(współczynnik p występuje w równaniu poprawki wówczas, gdy wyraz wolny la_lCp ~ ^a<ixi‘ “^aLCP jest wyrażony w jakiejś mierze kątowej).

z jednakowym błędem średnim pomiaru m_h - 0.02 (m).

Wysokości reperów R_{, R-, są znane i wynoszą: H_R( ~ 100.127 (m),    « 115.430 (m).

Wyrównać tę sieć oraz obliczyć:

1)    błędy średnie wyrównanych wysokości,

2)    błędy średnie wyrównanych przewyższeń h^łin,

3)    błąd średni funkcji a>-h\ + 2h₂.

Obliczenia wykonać stosując: a) rozwiązanie nieoznaczone, b) rozwiązanie oznaczone.

253