266 (33)

200 praktyczne znaczenie ma tylko uproszczona metoda obliczania pozwalająca w prosty sposób określić orientacyjną wartość współczynnika ekranowania według znanych wymiarów ekranu i rdzenia oraz początkowej przenikalności magnetycznej materiału ekranu. Pomijając ekranowanie wywoływane przez prądy wirowe, co jest dopuszczalne dla częstotliwości dziesiątek i setek *herców, oraz wprowadzając pewne założenia, możemy otrzymać wzory obliczeniowe o dokładności dostatecznej dla celów praktycznych.

Dla uproszczenia zagadnienia założymy, że pole po otoczeniu transformatora ekranem pozostanie takie samo jak było przy transformatorze bez ekranu oraz że cały strumień zakłócający $*, przechodzący przez rdzeń transformatora nie ekranowanego, jest równy strumieniowi przenikającemu do powierzchni ekranu położonej naprzeciwko jarzma rdzenia. Strumień ten rozdziela się na dwie części: jedna przebiega przez materiał ekranu, druga poprzez szczelinę powietrzną wchodzi do rdzenia transformatora. Strumień wchodzący do rdzenia ‘!’,r jest tylokrotnie mniejszy od strumienia w materiale ekranu, ilokrotnie oporność magnetyczna ekranu R, jest mniejsza od oporności magnetycznej szczeliny R_p. Z tego widać, że po zastosowaniu ekranu strumień magnetyczny wchodzący do rdzenia maleje w stosunku

-f-= 1 + ^    (XVI. 10)

4>„    ^ R.    ^K    *

Oporność magnetyczną ekranu można w przybliżeniu uważać za równą

R

8, V.

(XVI. 11)

gdzie: l, — połowa długości obwodu ekranu prostokątnego w płaszczyźnie równoległej do strumienia zakłóceń (rys. XVI.8), (cm); p_t — długość obwodu ekranu w płaszczyźnie prostopadłej do kierunku pola zakłóceń, (cm);

8, — grubość ekranu, (cm);

— początkowa przenikalność magnetyczna materiału ekranu (Gs/Oe).

Oporność magnetyczną drogi poprzez rdzeń można w przybliżeniu wyznaczyć ze wzoru

(XVI. 12)

* ■ v%

gdzie: 8p — odległość rdzenia od ekranu w kierunku linii pola zakłócającego (z jednej strony);

— grubość rdzenia;

l — długość jarzma rdzenia w kierunku prostopadłym do pola zakłóceń (równa sumie yj + 2b + 2y_;ł).

Mianownik wyrażenia (XVI.12) przedstawia powierzchnię rdzenia prostopadłą do linii pola zakłócającego; oporność magnetyczną samego rdzenia, jako bardzo małą w stosunku do oporności szczelin, pomijamy.

Po podstawieniu wartości R, i R_fi do wzoru (XVI.10) i założeniu, że stosunek ‘I*, do ł„ jest równy współczynnikowi ekranowania y, otrzymamy

(XVI.13)

Przy wartościach współczynnika ekranowania większych od 20 można wzór powyższy uprościć przez pominięcie jedynki.

Jak wykazały liczne pomiary, wzór (XVI.13) daje wyniki zgodne z pomiarami, jeżeli szczelina między rdzeniem i ekranem nie przekracza 3 -T- 5 mm, a więc wartości w praktyce najczęściej spotykanych. Wzór ten pozwala obliczyć współczynnik ekranowania prostokątnego ekranu, zamkniętego ze wszystkich stron, z materiału magnetycznego o jednakowej grubości. Ekrany otwarte z dwóch stron ekranują znacznie słabiej od zamkniętych i dlatego stosowanie ich jest niecelowe.

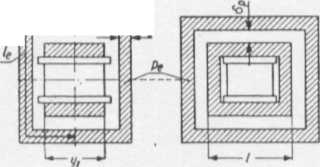
Rys. XVI.8. Wymiary potrzebne do obliczania współczynnika ekranowan a ekranu z materiału magnetycznego

Przy obliczaniu współczynnika ekranowania ekranu podwójnego oblicza się według wzoru (XVI.13) współczynnik ekranowania transformatora przez ekran wewnętrzny, a potem znajduje się współczynnik ekranowania ekranu wewnętrzne-go przez ekran zewnętrzny. Iloczyn obu współczynników stanowi wartość współczynnika ekranowania podwójnego. Dla przybliżonego wyznaczenia wartości współczynnika ekranowania ekranu wewnętrznego przez ekran zewnętrzny można również posłużyć się wzorem (XVI.13); wtedy jednak ekran wewnętrzny zastępuje się rdzeniem o takiej powierzchni boków jarzma, jaką ma rzeczywisty transformator (ten sam iloczyn Itya), i o odległości od ekranu równej odległości między ekranami. Z takiego obliczenia zwykle otrzymujemy liczby nieco większe od rzeczywistych wskutek nieuwzględnienia tego, że linie pola zakłócającego nie są równoległe; dokładniejsze obliczenie jest jednak zbyt skomplikowane dla celów praktycznych.

Obliczmy dla przykładu ekran złożony z dwóch prostopadłościanów wkładanych jeden w drugi, zwiniętych z taśmy permalloyowej o grubości 0,4 mm w 3 warstwy (całkowita grubość ft • 0.12 cm): prostopadłościany tworzą zamknięty ze wszystkich stron pojedynczy ekran. Przenikalność początkowa zastosowanego per-malloyu przy małych częstotliwościach wynosi 5000 Gs/Oe. Wymiary rdzenia transformatora są następujące: 1/2 ⁼ 1.5 cm, l = 4 cm; odległość rdzenia od ekranu w kierunku linii pola zakłócającego ó/» = 0 25 cm. obwód ekranu prostopadły do pola p, = 18 cm, pół obwodu równoległego do pola = 9 cm. Po podstawieniu tych danych do równania (XVI 13) otrzymamy

y

1    ,    2 8p p, 8, p—p

^,+    57T.—

0,5 • 18 • 0,12 • 5000

14--₄-7 , _s~₉-0*100, fj. 40 dB

Pomiary ekranu i transformatora o powyższych danych dały wynik 39 dB dla częstotliwości 100 Hz,

W tablicy XVI.1 podano rzędy wielkości współczynników ekranowania różnych ekranów i zobrazowano wpływ wymiarów transformatora na ekranowanie.