273 (25)

my. Ze w danej chwili czasu n populacja liczy sobie P_m osobników. Nazwijmy szybkością wzrostu populacji wielko# okrc<loną wzorem:

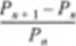
Najprostszy model rozwoju populacji zakłada. Ze szybko# wzrostu populacji jest stała. Wówczas przyrost wielkości populacji jest wprost proporcjonalny do aktualnej wielkości populacji. Ten model oznacza jednak stały wzrost populacji. Vcr-hulst załoZył natomiast. Ze wielko# populacji jest proporcjonalna do różnicy między maksymalną możliwą wielkością populacji S (wielko# populacji może być na przykład ograniczona zasobami pokarmowymi) a aktualną wielkością. Innymi słowy. populacja rozwija się szybciej, jeśli msza ekologiczna do opanowania jest duża. Możemy zatem napisać:

	(10.2)
Po odpowiednich przekształceniach otrzymujemy:
	(10.3)
Po podzieleniu przez N równanie przyjmuje postać:
A..I = '/».<! -Pj-	(10.4)
fdjJć pm • 4? otmcł.a ułarark maktymiinei »telkotfci pofut»cii

Otrzymane równanie, zwane równaniem logistycznym, pozwala wyliczyć rok po roku stan populacji na podstawie jej wyjściowej wielkości, liczby osobników w roku ubiegłym oraz stakj r. Zwróćmy uwagę. Ze stan układu jest dany dwoma zmiennymi p₉ oraz p„_t. Tak więc przestrzeń fazowa lego układu da się przedstawić na płaszczy źnie.

Ten prosty model rządzący wielkością populacji, choć znany był od dawna, nie ma analitycznego rozwiązania, jednak wielko# populacji w następnym roku można łatwo obliczyć nawet za pomocą kieszonkowego kalkulatora na podstawie wielkości populacji w danym roku. Nikt me podejrzewał. Ze równanie to może kryć w sobie jakieś niespodzianki. Spodziewano się. Ze w każdym przypadku układ bądź wpadnie w regularne oscylacje, bądź też dojdzie do stanu stacjonarnego Nikt więc nie podejmował żmudnych obliczeń. Zęby się o tym przekonać. Pierwszym uczonym. który zaczął systematyczne badania tego prostego równania, był Rohen M. May. Szybko /rozumiał on znaczenie szczególnych chaotycznych własności tego równania różnicowego i jest obecnie uznawany za jednego z pionierów teoni cha-

Zbadajmy zatem zachowanie takiej populacji dla wybranej wielko#! początkowej p₀ ora/ kilku różnych parametrów r.

273