276 (38)

452

Eliminując zmienne p₂, v₂ przez podstawienie ze wzorów (XII. 19) i (XII.22), dochodzimy do reiacji

której lewą stronę z uwzględnieniem (XII. 19) można przedstawić w postaci:

X

(XII.24)

ej . x .

2⁺—l^P'^V'-'°‘

j P0<^V0c

(XII.25)

Porównując (XII.25) z prawą stroną równania (XII.24) znajdziemy

Z równania (V.42) wiemy, że

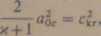
(XII.26)

Wzór (XII.26) orzeka, że prostopadłe uderzenie kompresyjne może wystąpić tylko w przepływie naddżwiękowym, gdy c, > c_kr, przy czym za uderzeniem musi być c₂ < c_kr. Przepływ przechodzi z naddźwiękowego w poddżwiękowy i ten przeskok jest tym większy, im większa jest liczba Macha przed miejscem uderzenia.

Analiza teoretyczna uwzględniająca właściwości fizyczne gazu rzeczywistego, a także badania eksperymentalne wykazują, że przebieg zjawiska jest bardziej skomplikowany. Uderzenie kompresyjne w dyszy wiąże się zawsze z mniej lub więcej intensywnym oderwaniem strumienia od ścianki [8, 43].

1.2.2. Praca dyszy dc Latała w zmiennych warunkach

Rozważmy ekspansję w dyszy rozszerzającej się od danych warunków początkowych p,, u, (rozumianych jako parametry całkowite) do zmiennego ciśnienia końcowego p₂ = var.

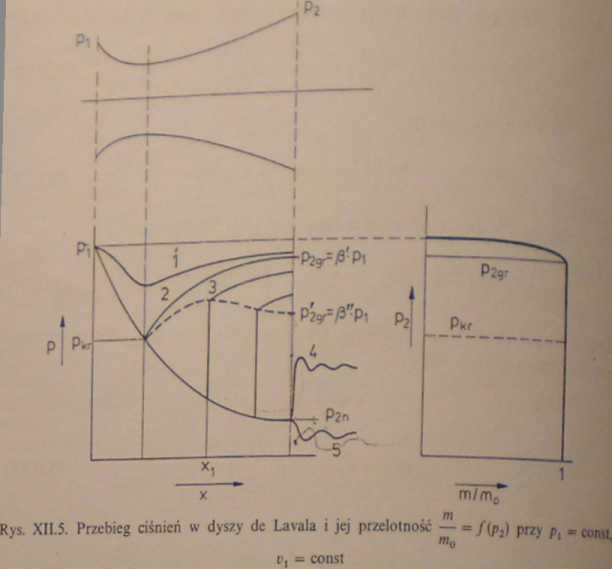
Oznaczmy przez p₂„ ciśnienie końcowe nominalne, na które dysza została skonstruowana. Analizować będziemy dyszę prostoosiową z przekrojem końcowym prostopadłym do osi (rys. XI 1.5).

Poczynając od p₂ = p, obniżamy stopniowo ciśnienie p₂ za dyszą. Przy bardzo małej różnicy ciśnień p, — p₂ panuje w całej dyszy przepływ pod-dźwiękowy. Z równania ciągłości (V.46) wynika, że w części zwężającej się musi zachodzić ekspansja, zaś w części rozszerzającej się — kompresja. Maksymalna

4*3