277 (37)

454

gdzie

e

•^k r

(5)

oznacza stopień rozszerzenia dyszy. Zastępując funkcję £ elipsą Bendemanna (XIf.5) podał Forner [433 prosty wzór na graniczny stosunek ciśnień:

(XI 1.27) dający dobrą zgodność z eksperymentem.

Znając ciśnienie graniczne p_2v — P'P\ możemy obliczyć graniczną prędkość wypływu z dyszy fgaz idealny bez strat). Zgodnie z (V.35.A):

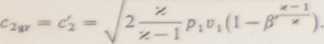
Przebieg ciśnień w dyszy w warunkach granicznych przedstawia linia 2 na rysunku XI 1.5. W tej sytuacji natężenie przepływu w dyszy osiąga maksimum, gdyż przy zadanych parametrach początkowych p_x, o, gęstość natężenia przepływu większa od panującej w najwęższym przekroju nie jest osiągalna.

Dalsze obniżenie ciśnienia końcowego p₂ nie powoduje więc żadnego zwiększenia natężenia przepływu w dyszy (rys. XI 1.5). W obszarze

P2n < Pa < Pa«r

następuje w części rozszerzającej się zbyt głęboka ekspansja, odpowiadająca przepływowi ponaddźwiękowemu, zaś w pewnym miejscu zachodzi prostopadłe uderzenie kompresyjne. Za tym uderzeniem przepływ staje się podkrytycz-ny (patrz równanie XII.6), połączony z kompresją czynnika w pozostałej części dyszy. Przebieg ten ilustruje linia 3 na rysunku XII.5.

W obszarze p₂ < p_2v obliczamy przebiegi ciśnień w następujący sposób. Przyjmujemy dowolnie położenie punktu K. w którym występuje uderzenie kompresyjne. Do tego miejsca przebieg ciśnienia w dyszy jest taki sam, jak w warunkach nominalnych, gdyż obowiązuje równanie ciągłości (V.46):

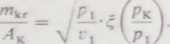
(7)

Z równania (7) można obliczyć ciśnienie p_K w miejscu A_K oraz odpowiednią prędkość c_K > c_kl. Stan gazu oraz jego prędkość za uderzeniem kompresyjnym określają równania (XI 1.3) i (XI 1.6). Od tego miejsca pozostała część dyszy pracuje jako dyfuzor. Stan termiczny czynnika i jego prędkość można łatwo obliczyć z równania zachowania energii i równania ciągłości:

W równaniu tym znamy m = A_K oraz parametry za uderzeniem c_K, p_K, p_k, natomiast niewiadomą jest ciśnienie p₂ w przekroju końcowym A_r (Podobne obliczenie możemy wykonać dla dowolnego przekroju za miejscem uderzenia A_t < A < A_v) Znajdując ciśnienie końcowe p₂ obliczamy prędkość wylotową przy tym ciśnieniu:

Przeprowadzając taką analizę dla wielu miejsc uderzenia kompresyjnego

A^_r c A u ^ A j.

otrzymujemy pełną charakterystykę przebiegu ciśnień (i prędkości) w dyszy w funkcji ciśnienia końcowego w obszarze

Pl ^< Plv

W skrajnym przypadku miejsce uderzenia leży w przekroju wylotowym A₂, przy ciśnieniu dolnym granicznym

00)

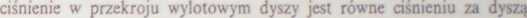
Pa, = Pi-

W przypadku skrajnym p₂ = p'_2v uderzenie kompresyjne zachodzi w przekroju wylotowym A_K = A₂.

Opisana teoria nie odpowiada na pytanie, jak zachowuje się dysza de Lavala przy ciśnieniu p₂ < p'_2fr Z badań doświadczalnych wynika. że w obszarze

Pu< Pi < P'i_v

przebieg ekspansji w dyszy jest taki sam jak w warunkach Pai = Pim po czym za dyszą następuje kompresja od p₂„

nominalnych.j do ciśnienIT

końcowego p_z (linia 4, rys. XII.5).

Wreszcie w obszarze p₂ < p_2n następuje w dyszy ekspansji do ciśnienia Pm = Pi* ^a pozostała ekspansja ma miejsce za przekrojem wylotowym dysz_; (linia 5 na rys. XI 1.5).

Zarówno uderzenie kompresyjne prostopadle, jak też proces ekspansji czy kompresji poza przyrządem stanowią przemiany obarczone dużymi stratami energii kinetycznej i połączone są z pulsacją ciśnienia (co stanowi zagrożenie wibracyjne łopatek wirnikowych). Z tych powodów dysza de Lavala wykazuje niekorzystną charakterystykę sprawnościową w zmiennych warunkach.