300 (10)

4)    Błąd średni wyrównanej odległości d₂ Biorąc pod uwagę, że

F- =03.-[0.764 0.645)

‘h

uzyskujemy

^m:_h = '»<)/^F]’(A⁷'PA)“^lF(?:? =»r₀₁/a₃.(A^TPAr^,aŁ -0.03 on)

5)    Błąd średni sumy wyrównanych kątów « i />’

Skoro -v = a + /(, więc

ds		da		* '
dX2\		2i		dX 2i
ds		da		3/J
dY2l		d Y2 1		dY2X

^: U4, -ł- a{.

F, =

105.921

62.838 •97.351

15.169

8.570

178.007

a następnie

m_s = m_(}    PA) ¹ F_f * 5'

Przykład 5.1.6

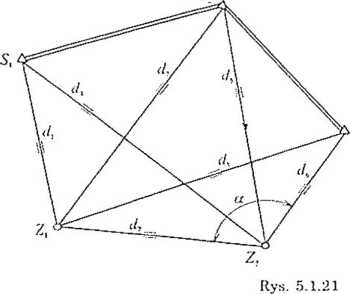
W celu wyznaczenia współrzędnych punktów Z₍ i Z-,, wykonano pomiar odległości d_x, d₁ oraz kąta a (rys. 5.1.21), uzyskując wyniki (podajemy też błędy średnie pomiaru):

df	= 151.581 (in)		df	= 269.408 on)
df	= 244.285	■—>/«] = 20 (mm)	df	= 233.510
df	= 255.235			= 148.655
df	= 182.453		a^ob	=11l^g49^c85^cc

Wyrównać tę sieć oraz wyznaczyć:

1)    błędy położenia punktów Z,, Z₇,

2)    błąd średni azymutu linii Z₇-Zj,

3)    elipsy ufności punktów Z₍, Z_? z prawdopodobieństwem y— 0.90.

W obliczeniach zastosować metodę oznaczoną.

A'frn)

>'( m)

S. | 1400.200 | 2389.750 ■V. I 1450.080 | 2550.150

•5\ | 1359.S80 ! 2640,360

•    i

współrzędne przybliżone

Z | 1250.180 | 2409.860 Z. i 1220.120 j 2589.820

Rozwiązanie

Przed przystąpieniem do wyrównania, ustalmy liczbę obserwacji koniecznych oraz sprawdźmy, czy istnieją obserwacje nadliczbowe. Do jednoznacznego ustalenia współrzędnych punktów Z_{ i Z-, są konieczne 4 obserwacje (/• - 4). Zwracaliśmy już wcześniej uwagę, że w klasycznych sieciach geode-zyjnych liczba obserwacji koniecznych jest równa liczbie wyznaczanych współrzędnych, a więc istotnie r 2 punkty ■ 2 współrzędne ~ 4. Ponieważ wykonano n - 8 pomiarów, więc są f n -r ~- 4 obserwacje nadliczbowe. Przyjmując za parametry, znane na poziomie przybliżonym, współrzędne punktów Z, i Z,, można sformułować następujący liniowy układ równań poprawek:

drf,	x=x°	ddi	x=x“	dd]	^rf**, x=x° ‘	3ć/i
		XI		3*2,		3>z2
dd2 , , ,	^Z, x.x°	r)dn 3rz,		ddo X	^£/*z, x=x°	ddn X:
dd7 v7 = -......	^d*z> X--X^(l	ód-j H-------— 3rz,	X./"^1	dd7 ^ł«z.	X-X° "	-b —------

x=x

^dy-/.-y

da

^dXz' !x-x°

g    da

P ^dx₇, ⁺ T_v......

¹ Oly,

X^X’^J

da

Z>

„ , da i ,, _p„^_i+    | _p j_Xzp

X-X^łJ

+ «⁰-a^,#6

301