004

Do tego samego wniosku dochodzi się, biorąc pod uwagę, że w stanie rezonansu susceptancja B dwójnika równa się zeru.

1.1.2. Rezonans amplitudowy

Rezonans amplitudowy jest to stan ekstremum wartości skutecznej prądu przy wymuszeniu napięciowym lub ekstremum wartości skutecznej napięcia przy wymuszeniu prądowym.

Np. przy zmianach częstotliwości, częstotliwość rezonansu amplitudowego wyznacza się z warunku koniecznego:

d(D

d(0

0, przy wymuszeniu napięciowym lub

0, przy wymuszeniu prądowym.

1.1.3. Rezonans fazowy, a amplitudowy

Tylko w układach szeregowym RLC i równoległym RLC oba zjawiska zachodzą przy tej samej częstotliwości. W obwodach bardziej złożonych zjawiska te zachodzą przy różnych częstotliwościach.

2.1 .Wywołanie zjawiska rezonansu i moce w obwodzie rezonansowym

W obwodzie zbudowanym z elementów R, L, C zjawisko rezonansu możemy wywoływać:

przy stałych parametrach R, L, C - poprzez zmianę częstotliwości zasilania

- przy stałej wartości częstotliwości zasilania - poprzez zmianę wartości elementów R, L lub C.

Obwód elektryczny R, L, C, będący w stanie rezonansu, nie pobiera ze źródła mocy biernej, gdyż zachodzi wzajemna kompensacja mocy biernej indukcyjnej

(coL|l|“ >o) z mocą bierną pojemnościową^--^|l|² <oj. Następuje zamiana pola magnetycznego cewki | W_L =— Li² J na energię pola elektrycznego kon

densatora

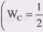
bez udziału źródła.

W stanie rezonansu ze źródła przekazywana jest do obwodu jedynie moc czynna P. która zamieniana jest w ciepło wydzielane na rezystancji R.

1.3. Przykłady wyznaczania częstotliwości rezonansu fazowego Przykład 1.

Rozpatrzone zostaną zjawiska zachodzące w układzie złożonym jak na rysunku

l.l.

Rys. 1.1

Dla przedstawionego połączenia admitancja wyraża się wzorem

R + jd)L

(I.3)

W wyniku przekształcenia

R - jtoL

Y = jcoC + —

r _ OL rMojl)²

R² +(o)L)^z R² + ((oL)² Warunkiem rezonansu jest, aby susceptancja dwójnika równała się zeru, czyli: