314 (31)

510

znajdujemy

Formula (XIII. 15) określa w poglądowy sposób, że naprężenie w łopatce zależy od gęstości materiału Q_m, odniesionej długości łopatki l/d oraz od prędkości obwodowej u.

Inną wygodną niekiedy formę wzoru (XIII. 14) otrzymujemy wprowadzając pola powierzchni osiowej zajmowanej przez łopatki

5 = ndl.

(XIII.16)

Zauważmy, że

n

co uwzględnione we wzorze (XIII. 14) daje

«.-_Tn

(XIII.17)

Wzór ten wskazuje, że naprężenie a, jest wprost proporcjonalne do powierzchni S. Związek ten ma ważne znaczenie przy projektowaniu ostatniego stopnia turbiny kondensacyjnej.

Wreszcie pisząc

S = n(rj—rj)

otrzymamy czwartą odmianę wzoru (XIII. 14):

o, = ie_m-w²(r?-r³.).

(XIII.18)

(XIII.19)

z której skorzystamy omawiając obliczanie naprężeń w łopatkach długich.

Pizy kład 1. Obliczyć naprężenia rozciągające w łopatce cylindrycznej przyjmując: d = 1 m, l/d — 0,25, czyli / = 250 mm, n = 3000 obr/min, Q_m = 8000 kg/m³ (stal).

Ze wzoru (XTII.4) wynika

a, = jifa&to* = --8000-0,25-1-314* -98,6-10* Pa =98,6 MPa.

Przykład 2. Obliczyć powierzchnię S zajmowaną przez łopatki, zakładając w = 314 rad/s (n = 3000 obr/min): g„ = 8000 kg/m³, <r_dop = 200 MPa.

Ze wzoru (XIII.17)

3.2. Łopatki ścienione

Naprężenie rozrywające w łopatkach wirnikowych można zredukować, jeżeli zamiast stałego przekroju wzdłuż promienia zastosuje się ścienianie łopatek.

Obliczmy przebieg naprężeń rozrywających się w łopatce w przekroju zmiennym wzdłuż promienia (rys. XIII.12).

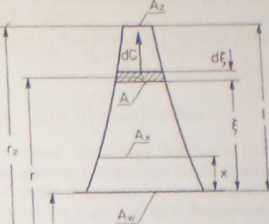
Rys. XIII. 12. Schemat do obliczania naprężeń w łopatce o zmiennym przekroju (ścienionej) Siła odśrodkowa elementu długości łopatki d( wynosi

(XIII.20)

dC = dnrru>² = Q_m-A(Ł)-dł;( »•„.+£)• to².

Całkując dC w granicach od £ = x do £ = I otrzymamy silę odśrodkową obciążającą łopatkę w przekroju odległym o x od miejsca zamocowania:

C_x = _L>_m oj² f -4(£)(r_w + £)d£.

(XIII.21)

(•>

Wywołuje ona w przekroju A_x naprężenie rozciągające /. »

Największe naprężenie rozrywające nie musi w tym przypadku wystąpić u podstawy, zależy to od postaci funkcji /!(£).

Najprostszy przypadek /4(£) = A_w = const odpowiada łopatce cylindrycznej. Wówczas we wzorze (XIII.22) znika A(()/A_x = 1 i redukuje się on do