316 (28)

514

a, = const

na całej długości łopatki nie jest możliwa, gdyż naprężenie a, na końcu łopatki musi wynosić zero. Do generowania naprężenia <7, = a„ = const w części równej wytrzymałości potrzebny jest odcinek o długości /, = r,—r_p, profilowany według innego prawa, najczęściej według zasady

A(r) = A_t = c onst.    (XI1I.24)

Pozostałą część o długości /₂ = /—/, = r_p—r_w określa warunek

^ai * ^ao ^m const.    (XIII-25)

Z równania równowagi wycinka o elementarnej długości dr otrzymujemy (patrz rys. XIII. 16)

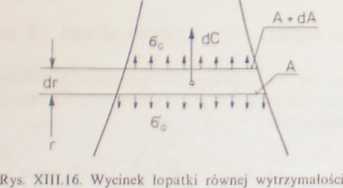
A ‘C_Q — (A dA)'odC,

stąd

a₀dA + dC = 0.    (XIII.26)

Równanie różniczkowe (XI11.26) rozwiązujemy podstawiając wartości elementarnej siły odśrodkowej

dC = dmrur = o_m^2, A-rdr,

rozdzielając zmienne

r/,4    o_ ,

— = -co²-rdr    (XIII.27)

A    <7₀

i całkując równanie (XII 1.27) w granicach od promienia wewnętrznego r_w dla dowolnego promienia r:

(XII 1.28)

In —=    eo²(r²-r²).

2o₀

Delogarytmując len wzór znajdujemy prawo zmienności przekroju łopatki w części równej wytrzymałości na rozciąganie:

A(r) — ył^eupT — ^~m^ł(r^ł—rjtn.    (XIII.29)

Na długości /, o stałym przekroju A = A, — const naprężenie rozciągające zmienia się i na promieniu podziału r_p, zgodnie ze wzorem (XIII. 19), wynosi

(X11I.3Q)

o_t(r_f) =

Z równania (XIIl.2£) wynika

t XI11.31)

(XII1.32)

OiirJ = °o = ^m"²(rp-r?_v)— Równania (XIII.30) i (XIII.31) łączy warunek

i M^rP).

stąd promień podziału

ri + rj ln AJA_t

(XIII.33)

\+YaAJA_t

Wartość ta jest przydatna dla konstruktora łopatki, określa ona podział na część o stałym przekroju /, i część równej wytrzymałości l₂.

Oznaczając

r_p = r_w+/₂    (XIII.34)

oraz promień średni

d₀    I 1

y = r₀ = r_w + - = -(d_B,+/), r₀ = r, d_Q = d otrzymamy ze wzoru (XI 11.33)

Skoro

H(H

1 +ln^:

r_t 1 +l/d r_w~ 1 —l/d’

(XI1I.35)

wobec tego