334 (30)

334

10. Dynamika punktu

początkowej jest równa zeru (vo = 0). Praca siły F będ^ równa

PRZYKŁAD 10.104

RYS. 10.63 _

PRZYKŁAD 10.105

RYS. 10.64

stąd

Prędkość graniczna

v_sr = lim v — 20 cm/s

*    r~* oo

f dr    ( 1

F = <łY<l2 ] ~2 — ^qiqi l +

•"O

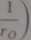
Klocek o ciężarze P jest przymocowany do sprężyny o stałej c. Klocek jest utrzymywany na równi dodatkową siłą tak, że w chwili początkowej sprężyna jest nieodkształcona. Znając współczynnik tarcia fi i kąt a znaleźć maksymalne przemieszczenie w dół po równi klocka, jeżeli zostaje on zwolniony bez prędkości początkowej (rys. 10.63).

ROZWIĄZANIE

Przyrost energii kinetycznej między położeniem A i położeniem B jest równy zeru (v_A = 0, v_B = 0). Praca sił działających na klocek między położeniem A i B wynosi

1 ₃

P sin ax_maks - P cos afi,x_maks - -cx;_wks -E_B~E_A- 0 stąd

2(P sina — Pp, cos a)

Dwa nieważkie pręty O A — l\ i OB = /$ (gdzie l\ > h) są złączone ze sobą na stałe pod kątem prostym. Na końcach prętów umieszczono kulki o ciężarach P\ i P2 (gdzie Pi > Ą). Znaleźć prędkość punktu B w chwili, gdy przechodzi on przez położenie poziome. Układ został puszczony z położenia I bez prędkości początkowej (rys. 10.64).

ROZWIĄZANIE

Ponieważ układ znajduje się w polu sił ciężkości, czyli w polu I potencjalnym, możemy zastosować zasadę zachowania energii mechanicznej

£14- Uj = En 4- Un    (i)

przy czym