348 (8)

oraz dalej

d_x =    )^-1 A^¹ A^r(BP"^lB^r)“¹ A = -<A⁷PA)~^!A^TPa|

K = -(BP''^!B^r)^_l(Ad_x +A) = -P(Ad* + A)    \

V - P~^lB^rk = P“^!P(Ad y + A) = Ad_x +^    i

co stanowi rozwiązanie klasycznego zadania wyrównawczego o postaci (gdy przyjmiemy, że A ~ L)

V = Ad_x +L

min{^(d,_Y) = V^rPv}= V⁷PV

^d.Y

Okazuje się więc, że w metodzie parametrycznej także można mówić o korelatach k. Zwróćmy uwagę, że ponieważ

K=-P(Ad*+A) lub k = -P(AdjY + L)

więc to interesujące rozpoznanie nie wnosi niczego nowego do znanego nam już z poprzednich rozdziałów rozwiązania. Pomimo tego, warto jednak odnotować, że w metodzie parametrycznej korelatami są równoważone estymatory poprawek, czyli K = -P(Ad^ +L) = -PV.

Niech teraz w równaniu BV+Ad^+A=0 zachodzi A~0. Wówczas

BV + Ad y + A = 0 o BV <- A _= 0

Wobec takiego założenia, rozwiązanie ustalające d _x nie istnieje, natomiast

K = -(BP"^łB^rr^ł(Ad_v +A) = -(BP"^lB^r)"¹Ai

> klasyczna metoda warunkowa

V = P"^łB⁷k

Przykłady

Przykład 6.1

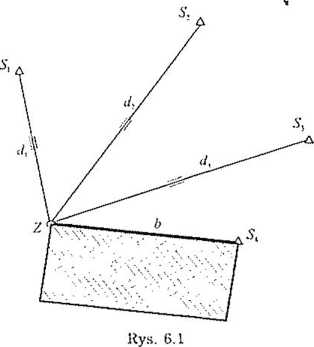
Punkty Z i S_Ą leżą na ścianie budynku długości b -- 182.312 (m), przy czym punkt S_Ą ma znane współrzędne w układzie {X, Y), podobnie jak punkty stałe £,, S-,, Sj. W celu wyznaczenia nieznanych współrzędnych punktu Z, zmierzono odległości ć/j, d₂> d_3> uzyskując wyniki (rys. 6.1):

d\^b =151.581 (m)    _ni[ — j2 (mm)

d^^h = 244.275 z błędami średnimi m₂ - 12

<7^=255.235    ^w3 = ⁵

Wyrównać tak uzyskaną sieć, przyjmując następujące współrzędne punktów:

	X (m)	V(m)
Si	1400.200	2389.750
^S2	1450.080	2550.150
S3	1359.880	2640.360
$4	1219.960	2589.840

Rozwiązanie

Wyrównane współrzędne punktu Z muszą spełniać warunek

J(Xs₄-xz)³+o 's,-y?.)² =»

Do wyrównania sieci zastosujemy więc metodę parametryczną z warunkami wiążącymi parametry.

Współrzędne punktów stałych oraz wyniki pomiaru odległości są takie same jak w przykładzie 5.1.3. Przyjmijmy zatem takie same jak tam wartości współrzędnych przybliżonych wyznaczanego punktu

Xz =1250.180 (m). Y§ - 2409.86 (m)

Pozwala to na przepisanie z przywołanego przykładu trzech pierwszych równań poprawek (dotyczących odległości d_l> d<_?> d_:i)

	v, =-coS/1^.( dx?
V=Ad* + L:	v2 =-cos^ dX/	Zv>2 'Z
	^v3=-cos 4v3<yz	, - sin +^3

349