36 (452)

70 Grzegorz Pękalski, Włodzimierz Dudziński

waż w stopie 11 występuje nadmiar cieczy w odniesieniu do wymagań stechiometrii (odcinek S- 2 jest dłuższy od odcinka ST)_t po reakcji perytektycznej pozostaje więc nadmiar cieczy (odcinek 7‘- 2), która nie przereagowała z kryształami fazy stałej y. Przebieg tej reakcji można więc zapisać następująco:

f-G ⁺ Ys AfBy + Lq

Konoda 3-3" narysowana w temperaturze niższej od temperamry przemiany pery-tektyczncj wskazuje na obecność faz/t*5> + U, tworzących strukturę stopu po przemianie.

W takim czasie reakcję przemiany perytektycznej w tym stopie można napisać następująco:

Lc +Ys L_G + A_xB_r

Korzystając przedstawionych poprzednio wiadomości, można zapisać reakcję przemiany dla stopu przed-perytektycznego położonego pomiędzy punktami S i 7*jako:

⁺ Ys Ys ⁺

Wróćmy ponownie do analizy stopu II w temperaturach niższych od temperatury przemiany perytektycznej. W obszarze TGUH po przemianie perytektycznej występuje ciecz L oraz AxBy. W miarę obniżania temperatury zmienia się (maleje) udział cieczy, a zwiększa się ilość zw iązku A_xBy. Faza ta ma stały skład chemiczny, natomiast skład chemiczny cieczy zmienia się wzdłuż linii GH. Przykładowo w temperaturze 3' -3 - 3"

3' - 3    .

y-r

udział cieczy wynosi ——— 1009^ , a w temperaturze 4' - 4 - 4" udział ten wynosi:

4'-4

%L *—--100% . W miarę dalszego obniżania temperatury ciecz osiąga skład punktu

4' - 4'

eutektycznego H i w analizowanym stopie zachodzi przemiana eutektyczna z nadmiarem fazy A \B_r, która pozostaje po przemianie, zapisana w sposób następujący:

Lff + AfBy r-r [A_xBy + ^)+ A_xBy

Po przemianie eutektycznej stop ten składa się z nietrwałej fazy międzymetalicznej A_xB_r oraz roztworu stałego p. Jego struktura zaś składa się z kryształów A_xB_r oraz eutek-tyki (A_xBy + P) - rys. 5.9. Udziały składników struktury stopu można określić za pomocą wykresu Sauveura (rys. 5.2d) lub można je też obliczyć, korzystając z reguły dźwigni.

Jak wynika z rys. 5.8, rzut punktu H na oś składów chemicznych (/f) wyznacza skład wyłącznie eutektyki (100% mieszaniny (A_xBy+ Pw-)). Konoda Y - H wyznaczona w temperaturze otoczenia umożliwia określenie odpowiednich udziałów fazy międzymetalicznej i eutektyki w tym stopie:    ¹

J

%A_xB_y =    100% , a %{A_xB_y + p)

5-Y Y-H'

100%.

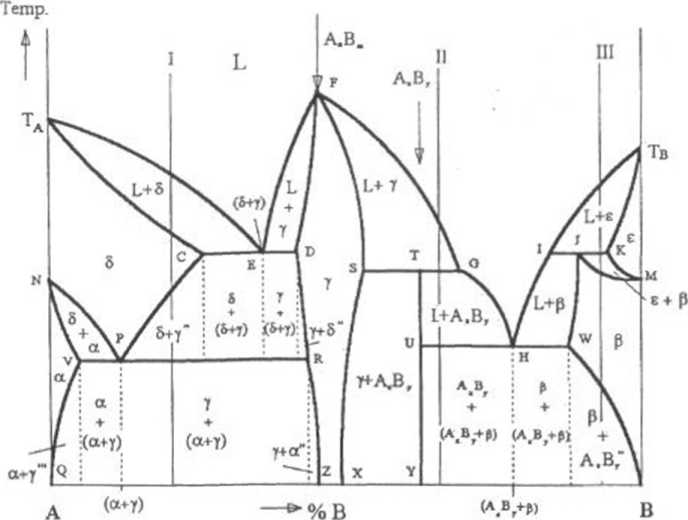
Rys. 5.9. Wykres równowagi układu dwóch składników A i B - opis strukturalny

Wyniki przedstawionej analizy przemian zachodzących podczas chłodzenia stopów I, II i II posłużyły do opisu strukturalnego wykresu przedstawionego na rys. 5.9. Opis ten jest ważny z tego powodu, że to właśnie mikrostruktury stopów są obserwowane w trakcie badań mikroskopowych. Korzystając zatem z wykresu równowagi, można określić rodzaj struktury, jaka będzie występować w stopie, w warunkach równowagi, w dowolnej temperaturze. Stosując regułę dźwigni, można także obliczyć udziały poszczególnych składników struktury, co z kolei ułatwia identyfikację obserwowanej mikrostruktury stopu.

Zadania do wykonania

Na podstawie otrzymanego rysunku rzeczywistego dwuskładnikowego wykresu równowagi należy:

1.    Opisać fazy występujące na wykresie i podać ich charakterystyki.

2.    Zidentyfikować przemiany fazowe występujące na wykresie, zapisać reakcje zachodzące podczas tych przemian oraz opisać wszystkie pola wykresu, z uwzględnieniem struktur powstających w wyniku przemian fazowych.

3.    Korzystając z reguły dżwigai, obliczyć udziały faz i struktur stopów w temperaturze podanej przez prowadzącego zajęcia.

4.    Naszkicować teoretyczne mikrostruktury stopów w temperaturze wskazanej przez prowadzącego.