33 (387)

2. Obliczenie procesu wypływu spalin z uwzględnieniem dużej amplitudy fal

Rozpatrując proces wylotu spalin trudno uniknąć dużego błędu, stosując założenie dopuszczalne np. podczas badania procesów zachodzących w układach ssących silnika, tzn. że proces ten przebiega przy małych zmianach ciśnienia i temperatury.

Obliczenie procesu wylotu spalin również w przypadku uwzględnienia dużej amplitudy fał ciśnienia i prędkości jest możliwe, a staje się ułatwione przy zastosowaniu jednej z istniejących metod graficznych, opartych zresztą przeważnie na pewnych założeniach upraszczających. Obliczenie powinno uwzględniać współczynniki przepływu uzyskane w trakcie pomiarów rzeczywistego przepływu w uproszczonych układach, gdyż umożliwia to ograniczenie zakresu prac badawczych nad prototypem, zwykle bardzo kosztownych.

Jedną z metod obliczania przebiegów fałowych, podaną przez R. Sau-era [95-97], można (jak m. in. dowiódł W. Endres [24]) dość łatwo zastosować w odniesieniu do fał ciśnienia o dużej amplitudzie, występujących w rurach wylotowych. Trudniej jest jednak uchwycić ich oddziaływanie na przebieg wymiany ładunku cylindra, zależny (podobnie jak ciśnienie w cylindrze) nie tylko od ruchu tłoka i przepływu ciepła, ale i od ilości wypływających spalin, tj. od prędkości ich przepływu w kanałach wylotowych (która ze swej strony zależy od różnicy ciśnień przed i za zaworem czy okienkiem). W dalszym ciągu zostanie opisana metoda Sauera, którą zastosować można również podczas badania przebiegu napełniania cylindra lub skrzyni korbowej silnika.

Wg Sauera zakłada się również, jak poprzednio, przepływ beztarciowy, przy czym rozpatruje się gaz idealny, zmiany stanu adiabatyczne i nie uwzględnia składowych prędkości poprzecznych do osi rury i nierówno-mierności rozkładu prędkości przepływu w poszczególnych miejscach rozpatrywanego przekroju. Unika się natomiast uproszczenia (niekiedy zresztą z powodzeniem stosowanego, co będzie d^lej wykazane), że istnieje liniowa zależność ciśnienia fali akustycznej i natężenia przepływu (p — W'p-a) i pisze równanie ruchu (impulsów) zgodnie z akustyczną „nieliniową” teorią fal o dużej amplitudzie;

6w

et

2

Ą---

/c-1

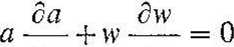
-'■s

ox cx

(36)

33

³ — Kordziński: Układy wylotowe