3 (248)

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja __operatorowa_

Przykład:

Stosując powyższe twierdzenia Laplace’a zapisać równanie różniczkowe opisujące obiekt sterowania w formie operatorowej:

dt

T •    + y^t) = k • UfU ’ równanie różniczkowe obiektu inercyjnego gdzie:

T - stała czasowa inercji, k - stały współczynnik.

Na podstawie twierdzenia 1. (o sumie funkcji) i 2. (transformata pochodnej) przekształcamy kolejno obie strony równania na formę operatorową:

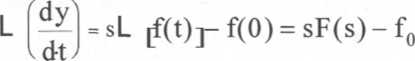
przyjmując f₀=0, y(t) —>Y(s), u(t) —* U(s), otrzymujemy operatorową postać równania:

Cwiczenia_automatyka_l.doc 2007-10-05 14

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja

Tablica wybranych transformat i oryginałów

	Transformata F|s)	Oryginał f(t)
1	1	4(0 (impuls Diraca)
2	1 1	l(f) (skok jednostkowy)
3	1 j»	i
4	1 #»	t*"^1 (a-D!
5	I m-t	t I T f°
6	i KTi+l)	t l-"T
7	1 rn+i)^1	t W' ^T
8	i (ł>+b"	r"(«-t)i
9	TU 7V+T	1 CO* -=■ T
10	T rv+f	+ T
11	1 (Tu+Wji+1)	"ru
12	itn.+tyrn+i)
13	i TW+2CT>+1
14	1 itTO+lCB+l)

Transform*ti1

Ćwiczenia automatyka 1 doc 2007-10-05 14

6