5 (195)

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja

_operatorowa_

1.    w wyniku pomnożenie transformaty wejścia u(s) przez transmitancję G(s) otrzymuje się transformatę wyjścia y(s), czyli odpowiedź, a przebieg czasowy odpowiedzi y(t) znajduje się jako transformatę odwrotną,

2.    określa właściwości dynamiczne obiektu np.- badanie stabilności na podstawie analizy sygnału wyjściowego,

3.    umożliwia wyznaczanie charakterystyk obiektu dynamicznego.

Podstawy obliczania transmitancji operatorowej

dⁿy(t) d^n_1y(t)    dy<t)

^an-^r^+an-i-^rr⁺ - ^+ai dt^+a°y® ⁼

d^ufl)    , dl<t) _t ..

——r+ ... ⁺bł^+b₀u(t)

dt^m "■' dt

Znajdujemy transformatę Laplace’a obu stron równania:

Po znalezieniu transformat obu stron równania, na podstawie poznanych twierdzeń

a_nsⁿ y{s) + a_n^s^nA y(s)+ ... a^y^ + ao y(s) =

= b_ms^m u^H-b^s™^-1 u(s)+ ... b₁su(s) + b₀ u(s)

Laplace’a otrzymujemy: gdzie:

y(s)=    [y(t)] = J y(t) e^st a u(s)= ^[u(t)]= J u(t) <z^_St

o    o    »

Po wyłączeniu przed nawias y(s) i u(s) otrzymujemy:

(a_nsⁿ+ a_n-i^sn_1+ - ^ai^s + ^ao) y(s) =

= (b_ms^m +b_m.₁s^ra"¹+ ... b_lS +b₀) u(s)

Po zsumowaniu wyrażeń w nawiasach otrzymujemy:

Ćwiczenia automatyka I doc 2007-10-05 14

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja _operatorowa_

m

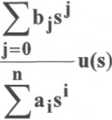
i=0

n    m

^TajS¹ y(s) = ^bjs^j u(s) => y(s) =

i=0    j=0

Podstawiając powyższe wyrażenie do definicji transmitancji otrzymujemy wzór do obliczania transmitancji:

Przykład 1. Obliczania transmitancji operatorowej

Dany jest obiekt dynamiczny liniowy (inercyjny tj. bezwładnościowy), stacjonarny, opisany równaniem różniczkowym: dy(t)

T ~ dt ' + y(t)= ku(t), gdzie: u(t) - sygnał wejściowy,

y(t) - sygnał wyjściowy,

T - stała czasowa, k - wzmocnienie

dokonujemy przekształcenia Laplace’a tzn. przechodzimy z dziedziny czasu -1 do obszaru zmiennej zespolonej s: t —> S :

L

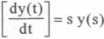
a

L D’(t)]= y(s), zatem

otrzymujemy na podstawie równania różniczkowego Tsy(s) + y(s) = k u(s), po wyciągnięciu y(s) przed nawias otrzymujemy: y(s)= [Ts + 1]= ku(s), dzieląc obustronnie przez u(s) i Ts + I, otrzymujemy: y(s) _ k u(s) Ts +1 ’

G(s)=    ₊ , w podobny sposób wyznacza się transmitancję innych układów

dynamicznych opisanych innymi określonymi równaniami różniczkowymi

('.■wiczenia_automatyka_I.doc 2007-10-05 14

10