4 (216)

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja _operatorowa__

Przykład a):

Dana jest funkcja zespolona: F(s) =    Określić funkcję oryginalną tj. w dziedzinie czasu t.

S

oryginał transformaty F(s)= -j-^y=f(t)

1©

fO dla t < 0    . • . j.

Impuls jednostkowy l(t) = \    J^o^owy

^w [ldlat^O

StKrll

Na podstawie 2 wiersza tablicy transformat i oryginałów znajdujemy:

y(t) = f(t) = L ^-1 fF(s)J = l(t), funkcja oryginalna to tzw. impuls jednostkowy.

Przykład b):

Dana jest funkcja zespolona F(s) = —r, określić funkcję oryginalną tj. w dziedzinie czasu t. Na s²

podstawie 3 wiersza tablicy transformat i oryginałów znajdujemy: y(t) = fU) = L'¹[F(s)] = t

2i    1

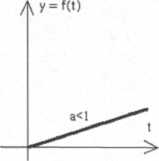
a jaka będzie postać funkcji oryginału dla funkcji zespolonej: F(s) = — = a- —

s²    S²

y(t) = fljt) = L ”‘[F(s)] = Lf a• -jj = aL

i    a

oryginał transformaty F(s)= —■,    oryginał transformaty F(s)=-^

A y-w

a=tga =

t

>

StarlO

Materiały do ćwiczenia nr 1.

Wprowadzenie do zajęć, podstawy rachunku operatorowego, transmitancja

_operatorowa_

Transmitancja i wyznaczenie transmitancji

Pojęcie transmitancji odnosi się do układu dynamicznego o następujących właściwościach:

1)    jednowymiarowy (o jednym wejściu u(t) i jednym wyjściu y(t)),

2)    liniowy,

3)    ciągły,

4)    stacjonarny,

5)    o stałych skupionych.

Układ taki opisuje zwykłe, liniowe równanie różniczkowe o stałych parametrach:

^an'

d"y(t)

dtⁿ

dⁿ-^]y(t)

dy(t)

^an-i-^r⁺ - ^+ai-^^+aoy(t) =

, d^mu(t) _L d¹"-'^)

= hm-+ h_m_l -

dtⁿ

dt’

m-1

^{+ bl}^^ + ^boU(t)

^an.^an-t, ^at. ^bni. ^bm-l. ^bl - parametry stałe Interpretacja tego równania jest następująca:

Obiekt dynamiczny zostaje pobudzony wymuszeniem (sterowaniem) u(t) dla t>0, a w wyniku wymuszenia (sterowania) powstaje odpowiedź: y(t).

Dla tak zdefiniowanych obiektów wprowadza się pojęcie transmitancji operatorowej.

Transmitancją operatorową obiektu dynamicznego,

0    wielkości wejściowej (sterującej) - u(t)

1    wielkości wyjściowej - y(t) nazywamy iloraz transformat Laplace’a: wielkości wyjściowej - y(s)

y (0) = 0, y*(0) = 0, . ,yⁿ(0) = 0

u (0) = 0, u (0) = 0, ...,11(0) = 0

i wielkości wejściowej - u(s) przy zerowych warunkach początkowych:

G(s) =    = Z®

^[u©] u(s)

Własności transmitancji:

8

Ćwiczenia automatyka l.doc 2007-10-05

14