401 2

401

9.3. Szybka analiza Fouriera

9.2-⁴

damy (po oczywistych zmianach oznaczeń) wzór

^CJ

przyjmijmy, że

-N"¹

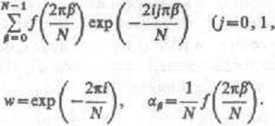
Możemy więc sformułować zadanie inaczej: dla./=0,1,    1 obliczyć wartości

N-l

(9,3.1)    */- £ «#^w* ^zic w*-l.

# = 0

Rozumiejąc przez „operację” mnożenie zespolone wraz z dodawaniem zespolonym, możemy rozwiązać to zadanie za pomocą schematu Homera (zob. przykład 1.3.3) kosztem ń' operacji na jeden współczynnik, a więc łącznie kosztem N² operacji. Natomiast szybka analiza Fouriera wymaga tylko JV(r₄-f r₂ + ... + r,) operacji, gdzie r_xr₂...r, =N. Jeśli zatem A'=2⁷=128, to liczba operacji z 2^,4= 16384 zmniejsza się do 2¹* I4» 1792. Algorytm (zwany FFT — Fast Fourier Transform) opracowali Cooley i Tukey w 1952 roku, jednak — jak w wielu innych przypadkach — zbliżone pomysły można znaleźć w licznych wcześniejszych pracach. W licznych dziedzinach zastosowań (telekomunikacja, analiza szeregów czasowych itd.) ten algorytm zupełnie zmienił poglądy na możliwości użycia metod Fouriera w obliczeniach komputerowych.

Rozważmy teraz przypadek szczególny A'=2\ Przyjmijmy, że    gdy fi jest pa

rzyste i fi*-2fi_x + 1, gdy fi jest nieparzyste (0<&1V—1). Wtedy wobec (9.3.1)

C)° £ <W»^a)^J'¹+ £ a_Vl+ł(w²)^y'^,w'.

#1-0    #i — 0

Niech <x będzie ilorazem, a j\ resztą z dzielenia j przez \N, tzn. niech będzie j=cr\N+)_l. Ponieważ    więc

(_Wy>=(*²;r^<ły>'^,(w²yⁱ'^ł -(w*r'V>'^,'^ł=(w²y^.

Jeśli więc przyjmiemy, że

f»0i)- £ a_2ft(w²Y'*'_t

# i-o

(9.3,2)

ł*-J

vc/i)— £ ^1(1^ (A-o. 1.....iN-1).

Sdiie (w*)"*.i_{f to}

«j“f>(/i) + *V(/i)    C/-0,1, ...,//-l).

Źc obliczanie ę>0\) i y(/i) oznacza dwukrotne wykonanie analizy Fouriera ¹ składnikami zamiast jednokrotnego, z,V=2* składnikami. Zastosujmy ten l P°mysl do tych dwóch, analiz Fouriera. Daje to cztery analizy Fouriera, każdą z 2*¹"²

Sy acmcrycroo