424 2

424

10. Optymalizacja

było najlepiej dopasowane do m punktów pomiarowych (t_ifyd    9

go

Nie można zastosować tu wprost metod z rozdziału 4, gdyż y (/, x) zależy niełiniow ^ parametrów x₂, x₅. Postawione zadanie można opisać jako rozwiązywanie nielwiJ^^ układu nadokreślonego

y(tf,x)asy_{ (i~l .2,...»m).

Jeśli pomiary mają równe wagi, to aproksymacja średniokwadratowa wymaga minimali zacji funkcji

(io.5.n    ?«= Y

i- I

Przykład 10.5.2. Niech l_lf f₂.....będą elementami próby pobranej z populacji

i niech/(r.«) będzie gęstością dla pewnej cechy tych elementów, gdzie a jest nieznanym wektorem parametrów. Zgodnie z zasadą największej wiarcgodności, a określa się znajdując maksimum funkcji

?(*)= FI/('!>«)•

Można to zrobić analitycznie tylko dla szczególnych rodzajów gęstości.

Rozważymy najpierw ogólne zadanie minimalizacji, jak w' drugim przykładzie, i założymy, żc pochodne cząstkowe można wyrazić w postaci analitycznej. (Specjalne techniki dla układów nadokreślonych będą podane w § 10.5.4). Zadanie redukuje się więc do rozwiązywania układu (zwykle nieliniowego)

(10.5.2)    *(*)«<?,

gdzie g(x)={dęfćx_l, c<p/tlx₂,..., cyjdxji^T jest gradientem funkcji <p. Można tu stosować metody z § 6.9, np. metodę Newtona opisaną wzorem

(10.5.3)    x_¥+₁*=x_y-H(x_y)g(x,),

gdzie H(x) jest macierzą odwrotną do jakobianu G(x) funkcji g:

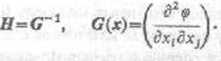
Macierz (7(jc) nazywa się też hesjanem funkcji <p. Zauważmy, że macierze G i H są symetryczne. Warunkiem dostatecznym na to, żeby rozwiązanie x równania (10.5.2) dawało minimum funkcji ę, jest nieujemna określoność macierzy G(x). To wTaz z możliwo®^ obliczania wartości funkcji <p stwarza korzystniejszą sytuację w porównaniu z dewoto)’¹⁰¹ układami nieliniowymi. Zauważmy, że obliczanie funkcji g jest zazwyczaj znacznie koszto* wniejsze niż obliczanie ę i że obliczanie G wymaga jeszcze w^rięccj pracy, szczególnie^svłe • ’ gdy n jest duże.

Przypomnijmy sobie, że zaletą metody Newtona jest jej zbieżność kwadratowa, zaleta jest okupiona następującymi wadami (zob. też § 10.5.3):