49 (220)

6.    Dla zrozumienia pojęcia stałej liczby elementów w danym zbiór* uczniowie eiemenly tego samego zbioru powinni przeliczać różnyn sposobami: od lewej do prawej i odwrotnie, od środka lub inneg miejsca w jedna, a potem w druga stronę, parami lub większyn grupami według kolorów, przeznaczenia, wielkości, układaniem rzedł mi po 3 lub 4 elementy, wkładaniem do pudelek ilp.

7.    Ćwiczenia w porządkowaniu według liczebności układu kilku zbioró. ma doprowadzić do rozumienia miejsca danej liczby między innyr) liczbami (program, s. 55) oraz rozumienia miejsca liczb mniejs/yc' i większych w stosunku do rozpatrywanej liczby, a jednoeześn zdawanie sobie sprawy przez uczniów z sąsiedztwa liczb.

2.5.2. Propozycja rozkładu materiału nauczania

W dziale 5 Klasyfikacja zbiorów ze względu na ich liczebność moż

przewidzieć następujące tematy lekcji:

1.    Porównywanie liczebności zbiorów poprzez łączenie ich w pary i prze czanie.

2.    Porównywanie liczebności zbiorów z użyciem określeń: tyle sam więcej, mniej, większy — więcej, mnieszy — mniej.

3.    Zestawienie elementów dwóch zbiorów z trzecim (przechodni ość ró ttoliczności i nierównolic/nośei).

4.    Porządkowanie różnych układów zbiorów według ich liczebności.

5* Sprawdzian, jego korekta i poprawa błędów.

2.5.3. Przykłady niektórych lekcji

Lekcja 1

Temat: Porównywanie liczebności zbiorów poprzez łączenie elementi u- pary i ich przeliczanie Cele: a) poznawczy — poznawanie zbiorów równo!icznych na konkretny przedmiotach, b) kształcący —kształtowanie pojęcia równoliczności i roz mienia określenia: tyle samo, umiejętności odnajdywania związków ilości wych między porównywanymi zbiorami przedmiotów, kształtowanie operac myślowych, c) wychowawczy — wskazywanie zalet umiejętności porówn wania ilościowego zbiorów w życiu, wyrabianie wytrwałości w samodzielny wykonani u zadań.

Metody: pokazu, praktycznego działania.

I nrniY organizacyjne. praca zbiorowa i zespołowa, indywidualna.

\radki dydaktyczne: piłeczki i kosz, szklanki i spodki, naczynia szklane i korale, pudełka i kasztany, plansze, klocki Dicnesa. przybory szkolne, kartki ze zbiorami, grzeb i eg lekcji:

t. ('więżenia utrwalające pojecie części wspólnej i złączenia zbiorów z wyko-, wstaniem rysunków zbiorów na tablicy i dużych klocków Dicnesa.

)„ Szacowanie na oko, czego jest więcej: piłeczek w koszu czy dzieci w klasie, samochodów czy kierowców {rysunek)? Propozycje, jak to sprawdzić.

\. Wprowadzanie sprawdzania zbiorów równoficznych przez łączenie ir pary. H stworzenie sytuacji problemowej czasie wkładania przez nauczyciela do dwóch naczyń szklanych ( wąskiego i szerokiego) korali po jednym do każdego naczynia. Po uzupełnieniu wąskiego nauczyciel pyta: Czy w każdym naczyniu jest tyle samo korali? Odpowiedzi będą prawdopodobnie różne. Teraz musi nastąpić wykładanie z naczyń przez porównanie (układanie) parami i stwierdzanie, że korali jest po tyle samo.

Wykonanie w zespołach podobnego ćwiczenia z kasztanami i dwoma różnymi pudełkami oraz sprawdzenie przypuszczenia z piłeczkami i dziećmi oraz samochodami i kierowcami.

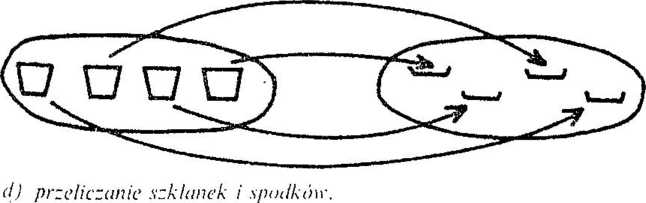
■I. Przyrównywanie szklanek do spodków przez łączenie w pary do pytania: Czy starczy szklanek i spodków dla czworga dzieci? a) rozwiązanie problemu przez łączenie w pary szklanki ze spodkiem b} narysowanie tej sytuacji na tablicy (szklanki ze spodkami), c) przedstawienie tej samej sytuacji na zbiorach przez przyporządkowanie szklankom z jednego zbioru odpowiednich spodków z drugiego zbioru za pomocą grafów strzałkowych. np.:

s. Porównywanie liczby Ó piłek i 5 uczniów

o i wykonywanie ćwiczenia poprzez pobranie przez uczniów piłek (bieżenie w pary),

95