49 (359)

Funkcje zespolone zmiennej zespolonej

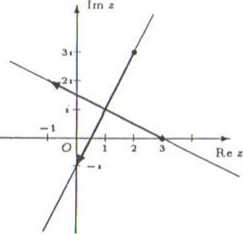
(ozwiązanie

‘rosła o równaniu z(<) = z₀ + zi t, gdzie € R, przechodzi przez punkt zo, a kąt niędzy nią a dodatnią częścią osi Ox jest ówny arg zj (z dokładnością do jr.) Po-ieważ arg («'zi) = - + argzj, więc szu-ana |>rosta prostopadła do prostej z(t) = + (—4 -f 2t)< dana jest wzorem

(0 = (2 + 3i) + (-2 — 4i)<, gdzie t g R.

naleźć obraz zbioru D przy odwzorowaniu w = /(z), jeżeli:

,    V.    o    ⁼

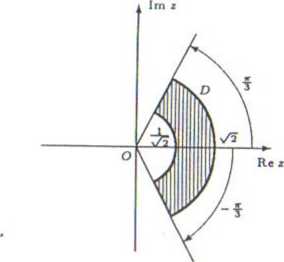
) D = |z g C : 1 ^ |z| ^ v/3, ^ ^ arg z <$ ^}, /(z) = 2iz². arysować zbiór D i otrzymany obraz.

)0=f,_SC: -L«|₂

ozwiązanie

) Mamy |iu| = |z²| = |z|². Stąd

^2 ^ l^zl ^ x/2 ą=>- — ^ |u>| ^ 2.

rdobnie arg w = 2 arg z, więc

* ^    ^ x    2rr    2t

- 3 ^ arg z ^ - ą=> - — $ arg u> ^ y.

rtem obrazem zbioru D jest zbiór

D' = {ui g C: i < |w| ^ 2, - y ^ arg w < yj •

Trzeci tydzień - przykłady

107

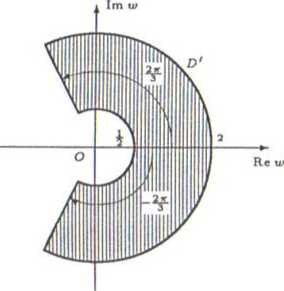
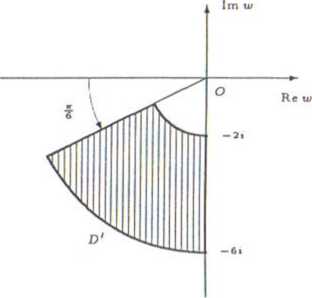
b) Mamy |u>| = 12 i z²1 = |2i| | z²1 = 21 z |². Stąd

1 ^ |z| ^ V^3 <=> 2 Sj |w| C.

Podobnie, dla pewnego argumentu ys liczby w zachodzi równość

V> = arg 2i + arg z² = ^ + 2 arg z.

Zatem

Tak więc obrazem zbioru D jest zbiór

D'={w&C: 2<H<6.    t}'

gdzie ip jest jednym z argumentów liczby w.

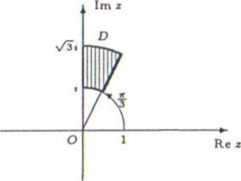
• Przykład 3.4

a) Znaleźć obraz okręgu |z — 1| = 1 bez punktu z — 0 przy odwzorowaniu w = -

* +1

b) Znaleźć obraz prostej y = — x przy odwzorowaniu w =

Rozwiązanie

a) Niech z / 0 oraz w yt 0. Wtedy

1    1

w = — <=> z = —. z    w

Stąd

Ir — 11 = 1 <=>--1=1

|1 ~ *>\ _ _t

|1 - ia| = ||

Obrazem jest więc prosta o równaniu Retu = - (symelralna odcinka o końcach 0, 1).