4 (1550)

Belki poddane zginaniu (rys. 4) mają przekrój prostokątny bxh.

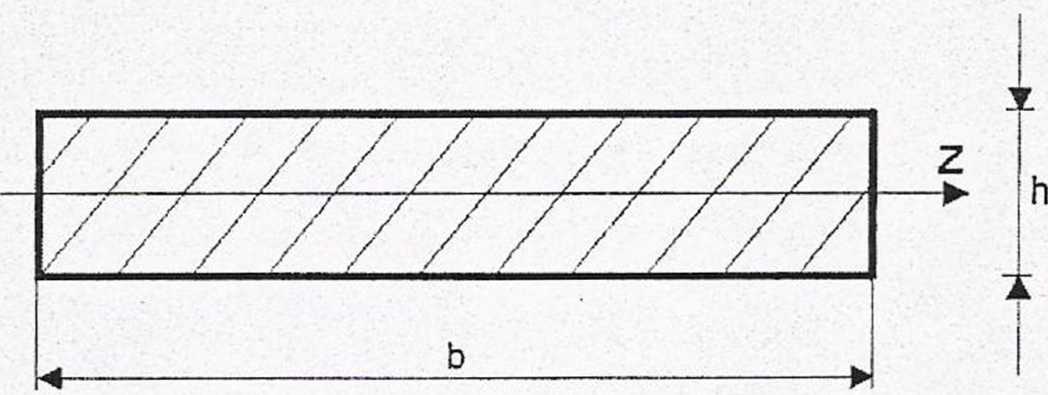
Rys. 3. Przekrój poprzeczny zginanej belki

Moment bezwładność i tego przekroju względem osi obojętnej z określa wzór:

J. =

bZ

~12

Po jego uwzględnieniu wzór ma moduł sprężystości E materiału belki przy czystym zginaniu ma ostatecznie postać :

2bh\f₂-f\)

gdzie:    P₂ = wartość „ górna” siły obciążającej w N,

P\ = wartość „ dolna” siły obciążającej w N,

/ =300 mm ( rozstaw podpór ),

a = 50 mm (odległość od siły do bliższej podpory ),

b = szerokość belki w mm ,

h = wysokość belki w mm ,

fi - strzałka ugięcia belki przy sile P₂, w mm ,

/ = strzałka ugięcia belki przy sile Pj , w mm .