4 (1855)

Średnia z odczytów wykonanych w dwóch położeniach lunety wolna jest od wpływu kolimacji.

Analizując wzór (?8) widzimy, że wpływ błędu kolimacji na odczyt koła poziomego zależy od wysokości obserwowanego celu. Przg lunecie w poziomie wpływ ten będzie się równał samej kolimacji (z=90 ), a im luneta będzie wyżej, tym będzie on większy.

Wpływ kolimacji na odczyty koła pionowego określa się ze wzoru

2

z - z’ = Az_c = ctg z*    (80)

Podstawiając do wzoru (80) z’ = 5°» c = 60", otrzymamy wpływ kolimacji na odczyt koła pionowego Az^ - OJ’1, Widzimy więc, że może on być całkowicie pomijany.

§ 9. Wpływ inklinacji na odczyt koła poziomego

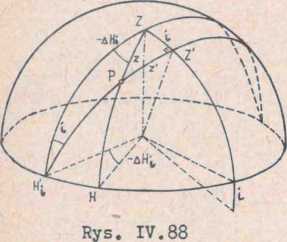
Inklinacją nazywamy nieprostopadłośó osi obrotu lunety do osi obrotu instrumentu. Oś celowa lunety zakreśli w tym wypadku płaszczyznę nachyloną pod kątem 90    - i do płaszczyzny hory

skąd

zontu. która w przecięciu z półkulą (rys.

IV.88) da koło wielkie przechodzące przez tzw. zenit instrumentalny Z*. Przy wycelowaniu na punkt wysoki P zamiast poprawnego odczytu poziomego H otrzymamy H^, który

obarczony jest wpływem inklinacji i. Wyznaczmy wielkość 41^ = H - H!!. Z trójkąta

ZPH!^ otrzymamy zależność

sin i

- sinAH^ sin (90°-z')

sin i

- sin A1L

cos z* sin z *

Zakładając, że sin z^,=^s sin z, dla małych wartości kątówAH, i i^, otrzymamy    ¹

= - i ctg z*.    (81)

Poprawiony odczyt koła poziomego będzie

H =Hj±ictg z’,    (82)

przy czym

dla I położenia lunety przyjmuje się znak plus, dla II położenia lunety - znak minus.

Wpływ inklinacji na odczyt koła poziomego, jak wynika ze wzoru, będzie wynosił zero przy celowych przebiegających w pobliżu horyzontu. Dlatego też przy pomiarach geodezyjnych błąd ten nie ma dużego znacze-

520