63 (149)

odpowiadających im słów (myśli, operacji w trakcie mówienia lub czyli nia). Dla przykładu: 6+1-7 (sześć, dodać lub plus, jeden, równa się kj jest siedem).

Należy uczniów stopniowo wdrażać do poprawnego odczytywali] treści formuły, a później do konstruowania manipulacyjnego na konkre nych przykładach (dokładania, dobierania, dosuwania. łączenia, dosvp] wania... łub zabierania, odsuwania ild.). słownego i symbolicznego form] Iowa nia oraz ich zapisu. Odbywać to się powinno najpierw- na przykładaj dodawania i odejmowania wielkości jednorodnych, a następnie różnyi wymagających zakwalifikowania ich do innej, ogólniejszej kategorii (nj 3 jabłka i 2 gruszki to 5 owoców).

Bardzo pomocne w dochodzeniu do formuły matematycznej są sch] maty Venna ukazujące dodawanie lub odejmowanie zbiorów rozlącznyc]

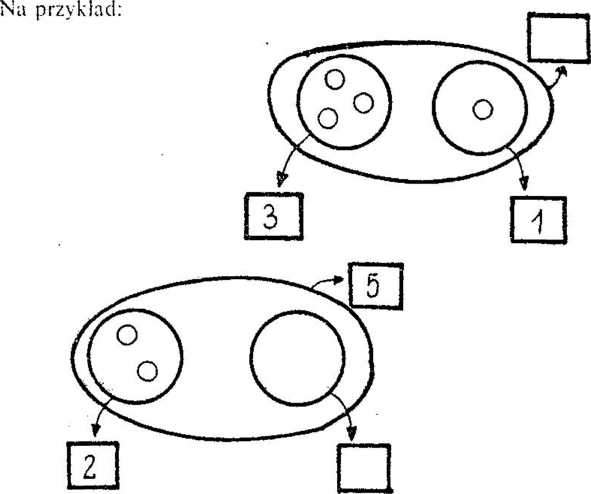
Ważne- jest uświadomienie sobie częstotliwości dobierania wielkoś< liczbowych do zadań (obliczeń) tak. aby wszystkie przypadki dodawani i odejmowania występowały, a te trudniejsze częściej.

Niżej podaję zestaw wszystkich przykładów- dodawania i odejmowani; w zakresie 10.

i i :	1 1 -i- 2	1 +3	1-1-4	i+5	1+6	1+7	1+8
> i	1 2 ±2	2-1-3	2 + 4	2+5	2 + 6	2 + 7	2-1-8
11	1 3 ± 2	3±3	3-1 4	3 + 5	3 + 6	3 + 7
-s i	1 4 + 2	4 ± 3	4 + 4	4 + 5	4 + 6
■i i	1 5 ± 2	5 ±3	5 + 4	5±5
a i	1 6 ;l; 2	6 ±3	6 + 4	6-5	6-6
/1	1 7 J; 2	i 7 i 3	7 — 4	7-5	7-6	7-7
K 1.	1 8 i- 2/	' 8-3	8-4	8-5	8-6	8-7	8-8
•> 1	1 9 - i	9 - 3	9-4	9-5	9-6	9-7	9-8
10 -	1 10-2	10-3	10-4	10 — 5	10-6	10-7	10-8

1+9

9 — 9

Zestawienie to zawiera 45 przypadków dodawania i 55 przypadków odejmowania. Jest to łączenie 100 przypadków działań dodawania i odejmowania. W tabeli tej mamy 10 przypadków dodawania i 15 przykładów odejmowania w zakresie 5, 9 przypadków dodawania (dopełniania) do 10

i 10 przypadków odejmowania od 10. Są to działania łatwiejsze. Natomiast pozostałe są trudniejsze, głównie ze względu na duże możliwości rozkładu lie/b na składniki. Stąd należałoby stosować je częściej.

W rozkładaniu danej liczby na składniki uczniowie po krótkim czasie mają przekonać się, że liczebność zbioru nic zmienia się pod wpływem zmiany układu (kolejności) jego składników. W ten sposób jednocześnie, |uż'od monografii liczby 4, poznają w sposób praktyczny prawo przemień-ności dodawania.

Układanie zadań do podanych obrazków na dodawanie i przekształcanie ich na zadania na odejmowanie doskonale utrwala pojęcie zależności wzajemnie odwrotnych i doprowadza stopniowo do abstrahowania i uogólniania lego pojęcia.

W dodawaniu liczb w zakresie 10 należy stopniować trudności, uwzględniając:

1.    Ćwiczenia wstępne polegające na wymienianiu kolejnych liczb, rozpoznawaniu ilości wykonywanych przez kogoś czynności, wykonywaniu określonej liczby czynności, w tym głównie: dosuwania, łączenia, dosypywania i t p.;

2.    Dodawanie przez doliczanie z zastosowaniem konkretów w odniesieniu do obu składników, np.: długość klocka równa się sumie długości dwóch klocków danych;

3.    Dodawanie przez doliczanie, z zastosowaniem konkretów w odniesieniu tylko do drugiego i następnych składników;

123