65 (205)

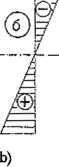
Ewentualne, dodatkowe momenty zginające AM_);£a, Asą spowodowane przesunięciem środka ciężkości przekroju klasy 4 '(rys. 3.34). Wówczas siła ściskająca N_u działa na mimośrodzie e_iN i dodatkowy moment zginający hM_iEJ wynosi:

Projektując ściskane lub/i zginane elementy prętowe (stupy, belki itpJ, a także płaskie konstrukcje prętowe (ramy, kratownice) powinno się uwzględnić ich współdziałanie z układami stężającymi.

^;,eó N_Elje_iN.

(3.77)

a)

BRUTTO

PRZEKROJE

	l oś ciężkości |

EFEKTYWNE

	_ strefa \
	nieefektywna
‘‘“oś ciężkości	przekroju
^eN	efektywnego

strefa nieefektywna

\^eN . — os	i
	oś ciężkości §
r~	przekroju ||~ efektywnego |

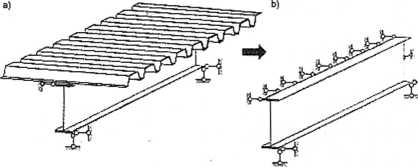
Belkę połączoną z blachą fałdową można uważać za stężoną w kierunku bocznym (rys. 3.35), jeśli spełniony jest warunek:

S>(EI„f_{2 +} GI_T+EI^)^, (3-78)

gdzie:

S - sztywność postaciowa (na jednostkę długości belki) poszycia z blachy fałdowej połączonej z belką w każdej fałdzie,

/„. - wycinkowy moment bezwładności przekroju belki, I_T~ moment bezwładności przy skręcaniu swobodnym belki,

l_z - moment bezwładności względem osi bezwdadności przekroju belki z - z,

L - długość belki, h - wysokość belki.

Jeśli blacha faldow<a jest połączona z belką w co drugiej fałdzie, to zamiast S przyjmuje się 0,2S.

Rys. 3.34. Efektywna geometria zginanego przekroju klasy 4: dwuteowego (a) i skrzynkowego (ii)

W PN-EN 1993-1-1 współczynniki interakcji k_yy k_vz, k_ można obliczać alternatywnie według Załącznika A do PN-EN 1993-1-1 - Metoda 1 lub według Załącznika B do PN-EN 1993-1-1 - Metoda 2. Załącznik Krajowy do PN-EN 1993-1-1 zaleca obliczanie współczynnika interakcji według Metody 2.

Przykłady obliczeń elementów zginanych i ściskanych wg PN-EN 1993-1-1 przedstawiono w [3-28], [3-30],

3.7.6. Ciągłe i dyskretne stężenia belek pełnościennych i o stałym przekroju

Projektując ściskane lub/i zginane elementy prętowe (słupy, belki itp.), a także płaskie konstrukcje prętowe (ramy, kratownice) powinno się uwzględnić ich współdziałanie z układami stężającymi. Zadaniem konstrukcyjnym układów' stężających jest skuteczne przeciwdziałanie utracie stateczności ogólnej (wybocze-niu lub zwichrzeniu) i obniżeniu nośności rozumianej jako giętny lub giętno-skrętny mechanizm zniszczenia ustroju. Rolę elementów stężających, skutecznie przeciwdziałających wymienionym formom niestateczności, mogą spełniać elementy' tarczowo-prętowe, trwale połączone z podpieranymi elementami konstrukcyjnymi lub stężenia boczne i/lub przeciwskrętne, dyskretnie zlokalizowane na długości elementów podpieranych.

Wymagania dotyczące sztywności postaciowej 5 (na jednostkę długości belki), ciągłego stężenia bocznego i sztywności obrotowej stężenia przeciwskrętnego poszycia z blach fałdowych, skutecznie przeciwdziała-jącego możliwości zwichrzenia belek, podano odpowiednio w Załączniku BB 2.1 oraz Załączniku BB 2.2 do PN-EN 1993-1-1.

Rys. 3.35. Ciągłe stężenie boczne z blachy fałdowej zespolonej łącznikami mechanicznymi z belką dwuteową: a) - model fizyczny, b) - model obliczeniowy

Sztywność postaciową 5 (na jednostkę długości belki) poszycia z blachy fałdowej połączonej z belką w każdej fałdzie, po obu stronach zakładki i na obu brzegach można obliczać ze wzoru:

5 = 100(h/F(50 + 10    [W,    ⁽³'⁷⁹⁾

"w

gdzie:

t - obliczeniowa grubość blachy fałdowej poszycia [mm],

b_ng - szerokość tarczy stężającej [mm], s - rozpiętość tarczy stężającej [mm], h_w - wysokość profilu poszycia [mm].

Belkę można uważać za skutecznie stężoną przeciw-skrętnie, gdy spełniony jest warunek:

M²

(3-80)

gdzie:

C_fl>„ - sztywność obrotowa (na jednostkę długości belki), której pas jest gęsto połączony z ciągłym poszyciem,

K_v = 0,35 - w przypadku analizy sprężystej,

K, =1,00- w przypadku analizy plastycznej,

M_plk - wartość charakterystyczna nośności plastycznej belki przy zginaniu.

W miejscach przegubów plastycznych, które powstają w procesie redystrybucji momentów zginają-

72 EUROKODY - ZESZYTY EDUKACYJNE Builcfera - PROJEKTOWANIE KONSTRUKCJI STALOWYCH

styczeń 2011