69 (28)

y'(x) = c'(x)e f^p(x)d^x _+c(x)e ^^P(x)dx(-p(x))

y' + P(x)y = c'(x)e~^Jp(x)dx + c(x)e~^JP(x)dx(-p(x))+p(x)c(x)e~^lP(x)dx =g(x) =>

c'(x) = g(x)e^Jp(x)dx =>c(x)= Jg(x)e^lp(x)dx+C =>y(x) = [Jg(x)e^Jp(x)dx +C]-e"^lP(xdx =>

y(x) = Ce"^lP(x)dx _+e^_lP(x)dx . Jg(x)e^Jp(x)dx -RORNJ Przykład 8.

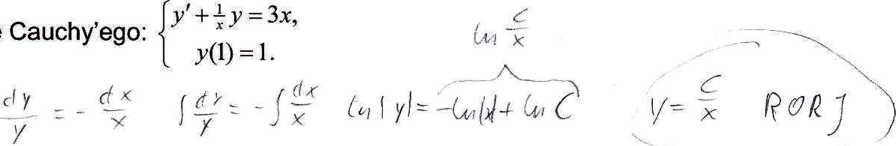
Rozwiązać zagadnienie

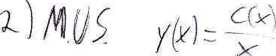
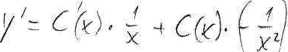
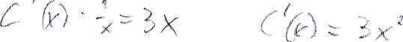
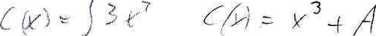
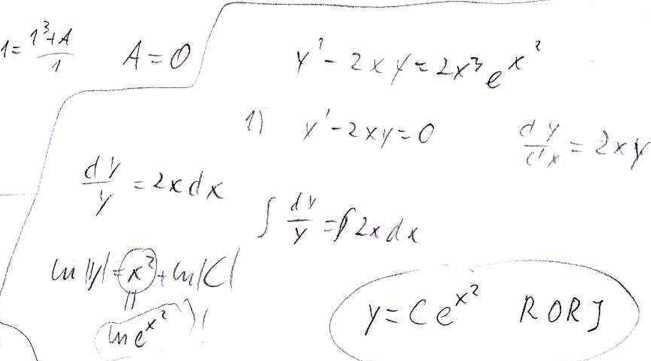
v

kom y - mr    y w* <

Przykład 9.

Rozwiązać równanie: 2ydx+(y²-2x)dy=0.

MAT2 Mechatronika Jan Nawrocki 69