7 (1009)

: składowe tego natężenia - wg klasycznej, newtonowskiej teorii wytła-a - określone są następującymi zależnościami:

n² D²hN sin tp cos(p

2

(3-3)

<?c

n Dh³ sin²(p dp

12r| ~E

(3.4)

e: D — średnica zewnętrzna ślimaka, h — >wania, N — prędkość obrotowa ślimaka, tp •

głębokość kanału w strefie - kąt pochylenia linii śrubo-

DJJt

powierzchnia cylindra ®

powierzchnia ślimaka (rdzeń)

wej ślimaka, rj — lepkość tworzywa, dp/dl — gradient ciśnienia wzdłuż długości ślimaka.

Można przyjąć w uproszczeniu, że gradient ciśnienia w strefie dozowania jest stały, tzn. że:

dp _

dl

L

(3.5)

-- V,

powierzchnia cylindra o>

gdzie: A/? — całkowity przyrost ciśnienia w strefie dozowania, L — długość strefy dozowania.

Wówczas, podstawiając związek (3.5) do równania (3.4) uzyskuje się zależność opisującą natężenie przepływu w postaci:

Q = aN-b

AP

(3.6)

powierzchnia cylindra

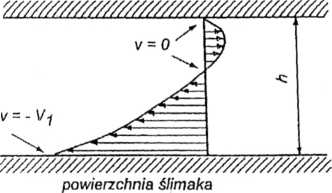
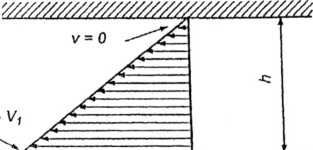
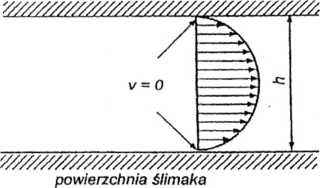
Rys. 3.13. Rozkład prędkości tworzywa w kanale ślimaka w przekroju wzdłużnym: a) przepływ wleczony, b) przepływ ciśnieniowy, c) przepływ wypadkowy; v — prędkość tworzywa, V, — składowa prędkości obwodowej ślimaka równoległa do zwoju, li — głębokość kanału

gdzie a i Z? są wielkościami zależnymi jedynie od geometrii ślimaka i wyrażają się wzorami:

ti¹ D²h sin<p costp

2

n Dh³ sin²<p 12L

(3-7)

(3.8)

Lepkość tworzywa ti , występująca w równaniach (3.4) i (3.6), jest funkcją temperatury i prędkości ści-

nania w tzw. charla

kanale ślimaka. W przybliżeniu można ją określić na podstav\XAt kterystycznej prędkości ścinania, która wyraża się wzorem

V

t

gdzie: y

— charakterystyczna prędkość ścinania, V_c = nDN - prędlO^C obwodowi ślimaka, h — głębokość kanału ślimaka.

Równanie (3.6), w układzie współrzędnych: objętościowe natężenie pi£6".. pływu—ciśnienie przedstawia linię prostą o ujemnym współczynniku k?^'³ wym, któia stanowi charakterystykę danego ślimaka (rys. 3.14).

Przepływ tworzywa w głowicy wytłaczarskiej zachodzi pod wpływe^^ ciśnienia 'vytworzonego w układzie uplastyczniającym wytłaczarki. Ciśniem^C to musi być ńa tyle duże, aby zostały pokonane opory przepływu stawiane przez głowicę. Całkowity spadek ciśnienia w głowicy wytłaczarskiej jest sumą spadków ciśnienia w jej elementach składowych (o określonym kształcie przekroju poprzecznego kanału).

Natężerie przepływu ciśnieniowego można okre-stawie znanego równania Hagena-Poise-

ślić na poci uille’a, któ j

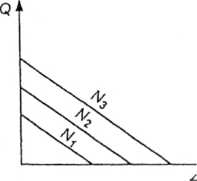
Rys. 3.14. Charakteryst) t-O-ślimaka dla różnych warto^ok jego prędkości obrotowej (N₃ >N₂> N_{)

e dla cieczy newtonowskiej ma postać

4p

(3.10)

Tl

gdzie: Q — objętościowe natężenie przepływu tworzywa, Ap — różnica ci nienia wywołująca przepływ, tj — lepkość tworzywa, K — wielkość charakt ryzująca geometrię kanału przepływu, tzw. przewodność kauału, która — prTijy kładowo — dla kanału o przekroju kołowym ma postać:    ^

K =

nJT 8 L

(3.11)

a dla kanału

o przekroju prostokątnym — postać:

WH³

K =

12L

(3.12

gdzie: K — przewodność kanału (odwrotność oporności kanału), R, W, H L ~ promień, szerokość, wysokość i długość kanału.

Warto zwrócić uwagę, że wzór (3.12) można z pewnym przybliżeniem j zastosować do obliczania przewodności kanału pierścieniowego, charakteryzo-uJn^i. wanego promieniem zewnętrznym R_z i promieniem wewnętrznym R_w. Wów - j czas, szerokość takiego kanału jest równa: W = n(R_z + R_w), natomiast grubość H = R-Rj