9 (844)

i

16

1.3 Modo! ś argument liczby zespolonej

Liczby zespolone

Moduł i argurr

© Definicja 1.3.1 (moduł liczby zespolonej)

Modułem liczby zespolonej z = x+iy. gdzie x,y € R, nazywamy liczbę rzeczywistą \z\ określoną wzorem:

def

Izl = \Jx² + y^:

a

- u

2-

o)

X X

J

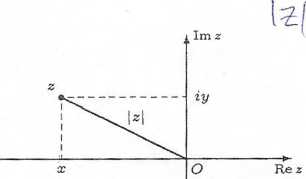
Rys. 1.3.1. Interpretacja geometryczna modułu liczby zespolonej.

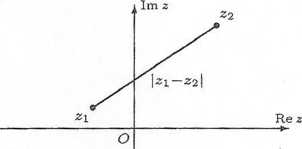
Rys. 1.3.2. Interpretacja geometryczna modułu różnicy* liczb zespolonych.

Uwaga. Moduł liczby zespolonej jest uogólnieniem wartości bezwzględnej liczby rzeczywistej. Geometrycznie moduł liczby zespolonej z jest odległością punktu z od początku układu współrzędnych (rys. 1.3.1). Moduł różnicy liczb zespolonych Z]_, z2 jest długością odcinka łączącego punkty zi,*2 płaszczyzny zespolonej (rys. 1.3.2).

O Ćwiczenie 1.3.2

Obliczyć moduły podanych liczb zespolonych:

1    y/3

a) z = -i; b) z = — 1 + 3i;    ^c)z=--*—;

11 Fakt 1.3.3 (własności modułu liczby zespolonej) Niech z, zi, Z2 € C. Wtedy

1. \z\ = \z\ = \—z\;

3. |*i • z₂| = |zi| ■ |z₂|;

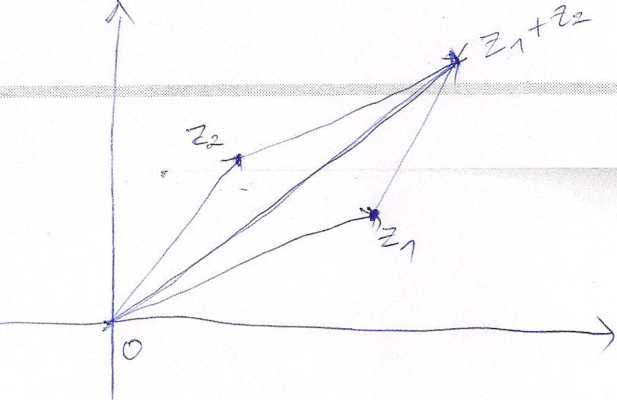
5. |zi + z₂| < |*i| + \z₂\;

7. |Rez| < |*|, |Imz| < |*|;

X

X

^Ry

Przy obliczanii: tożsamość:

O Ćwiczenie 1.3.'

Obliczyć moduł

^a) (1 + 2ż)(3 —

Snterpretat

d) z = -5-12*.

<W) 'Re a

a

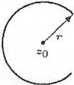
2. z • z = |zj² ;

4. — = o ile z₂ ^ 0; ^z2 \^z2\

6. | |z! j - |z₂j | < \z! - *a|; 8. |Re (*iz₂)| < M |z₂|.

Uwaga. Warunki podane w punktach 3. i 5. powyższego faktu prawdziwe są także dla dowolnej liczby odpowiednio czynników i składników. W szczególności mamy \zⁿ\ = \z\ⁿ dla n G N. Nierówność 5. jest nazywana nierównością trójkąta (rys. 1.3.3).

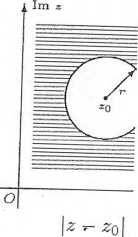
\^z - ^0