CCF20090516000

OPERACJE SYMETRII

Istotną, zauważalną cechą kryształów jest ich zewnętrzna symetria czyli prawidłowe powtarzanie się w przestrzeni jednakowych pod względem geometrycznym (kształt i wielkość) ścian, krawędzi oraz naroży.

4. A. Ryberczyk-Pirck

Podstawowe pojęcia klasycznej teorii symetrii kryształów

Przekształcenie (transformacja, operacja) wykonane na zbiorze {U} - przepis, za pomocą którego punktom zbioru {U} przyporządkowuje się punkty zbioru {U’}

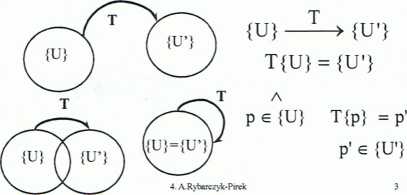
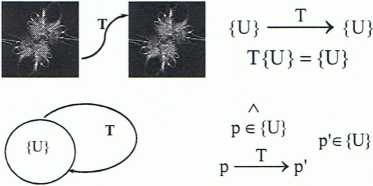
Jeśli po wykonaniu transformacji zbiór {U} pozostaje niezmienny - było to przekształcenie symetryczne względem tego zbioru, a każdy punkt zbioru {U} przekształca się w inny punkt również należący do tego zbioru

4. A Rybarczyk-Pirck    5

Symetria - właściwość figury geometrycznej polegająca na tym, że przy określonych zmianach położenia figury, nowe położenie pokrywa się z położeniem pierwotnym

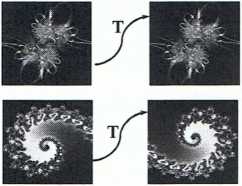
Gdy istnieje tylko jedno takie położenie, w którym figura nakłada się sama na siebie, wówczas jest ona asymetryczna.

4. AR>t>erczyk-Pirek    4

Przekształcenie symetryczne (operacja symetrii) -

transformacja doprowadzająca do nałożenia się figury lub jej części na inną figurę lub inną równą pierwotnej część figury.

Część symetrycznie niezależna wzoru (motyw) -

podstawowa część symetrycznego wzoru, która po wielokrotnym przekształceniu symetrycznym odtworzy cały wzór

	Po wykonaniu operacji symetrii dany element figury pokrywa się nie /	4 b * « -V
p	ze sobą, lecz z innym \ elementem figury pierwotnej	' f : V m m

2 elementy symetrycznie równoważne

równoważne

4 elementy symetrycznie równoważne

4. ARybarczyk-Pirek