CCF20130109013

Przy podziale złożonej figury płaskiej na figury proste, których współrzędne środków ciężkości y„ z, są znane, zależności (2.1) i (2.2) przyjmują postać:

^Sy=Yj^Ai^zi’ i	= X ^A‘^y‘ i	(2.3)
Y.^A>y-‘	1^A*
^}c ’	- XV	(2.4)

/ /

Jeżeli figura płaska ma oś symetrii, to środek ciężkości leży na tej osi, w przy padku dwu osi symetrii - środek ciężkości znajduje się w punkcie ich przecięcia.

d.    Momenty bezwładności pola względem osi w m⁴

Momentem bezwładności pola A względem osi leżącej w jego płaszczyźnie na zywamy sumę iloczynów elementarnych pól cIA przez kwadraty ich odległości od tej osi, obejmującą całe pole:

I = \z²dA, I, = \y²dA.    (2.5)

(a)    (A)

Momenty bezwładności względem osi są zawsze dodatnie.

e.    Moment bezwładności pola względem punktu w m⁴

Biegunowym momentem bezwładności pola A względem punktu (bieguna) na zywamy sumę iloczynów elementarnych pól dA przez kwadraty ich odległości od tego punktu (bieguna), obejmującą całe pole:

lo =jp²dA.    (2.6)

(A)

Biegunowy moment bezwładności ma zawsze wartość dodatnią.

Z rysunku 2.1 wynika, że: p² = y² + z², wobec tego

I₀= JV +z²)dA = l_y + l_z.    (2.7)

(a)

f.    Odśrodkowy moment bezwładności (moment dewiacji) w m⁴

Odśrodkowym momentem bezwładności pola A względem układu osi leżących w płaszczyźnie pola nazywamy sumę iloczynów elementarnych pól dA przez ich odległości od obu osi, obejmującą całe pole:

j yzdA.

(2.8)

(A)

Moment odśrodkowy może przyjmować wartości dodatnie, ujemne lub może i. ■ równy zeru.

Momenty bezwładności charakteryzują opór, jaki stawia siłom odkształcającym .l im. element konstrukcji w zależności od kształtu i wielkości jego przekroju po-

I>1 /et /nego.

Promienie bezwładności w m

Promienie bezwładności określa się następująco:

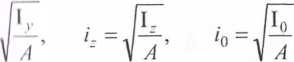
! ! / A MOŻNOŚCI MIĘDZY MOMENTAMI BEZWŁADNOŚCI I' IGURY WZGLĘDEM OSI RÓWNOLEGŁYCH

I klml osi yo, Zo ma początek w środku ciężkości figury. Osie układu y, z sąprze-. li i o, le równolegle względem y₀, zo o odcinki a i b, jak pokazano na rysunku 2.2.

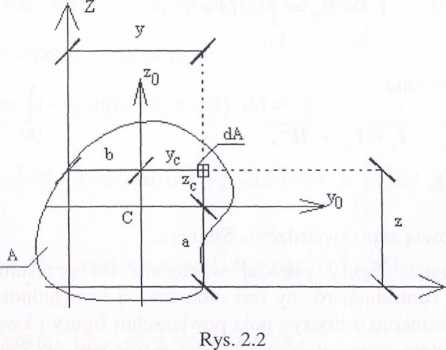
I m, «Izy współrzędnymi dowolnego pola dA w obu układach zachodzą zależności:

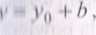
■•o

i a.