26028

Na rysunku 2 przedstawiono przyjęty układ osi, podział całej figury na figury składowe oraz położenia środków ciężkości figur składowych.

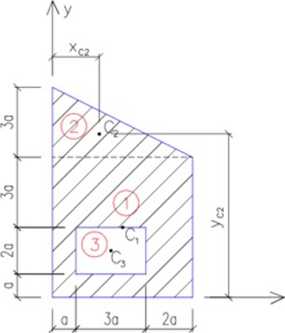
Rysunek 2

Statyczne momenty bezwładności względem osi x i y obliczamy sumując statyczne momenty bezwładności wszystkich figur składowych, przyjmując dla figur będących otworami pole powierzchni ze znakiem ujemnym:

S_t = 6a 6a 3a + — 6a 3a ^ 6a + — 3a j + (-3a2a)^a + — 2a j = 108#³ + 63a³ - 12a³ = 159a³

S_y = 6a6a3a + ^6a3a jóa + (-3a2a)^a + -^-3« j = 108<z³ + 18a³ - 15a³ = 11 la³

Pole powierzchni całej figury wynosi:

A = 6a6a + — 6a3a + (- 3a 2a) = 36a² + 9a² -6a² = 39a²

Współrzędne środka ciężkości całej figury w przyjętych osiach (x, y) wynoszą zatem odpowiednio:

lila³ 111

39a

39

a = 2.85a

S,    159a³ 159

V. = —- =    , = -TTa = 4.08a

A    39 a'    39

Obliczone wartości współrzędnych środka ciężkości znajdujemy na rysunku w układzie osi (x, y) uzyskując środek ciężkości - C (patrz rysunek 3). Położenie środka ciężkości figury nic zależy od przyjętego wstępnie układu osi, ani sposobu podziału na figury składowe.

2