CCF20101219006 (5)

Momenty statyczny pola figury płaskiej w układzie kartezjańskim względem osi x, y określamy wzorami:

S_x = J ydA

A

S_y = J x dA

A

Moment bezwładności ciała płaskiego względem osi prostopadłej do jego płaszczyzny równa się sumie momentów bezwładności względem dwóch osi wzajemnie prostopadłych, leżących w jego płaszczyźnie.

/ = /,+/,

Biegunowy moment bezwładności jest sumą osiowych momentów bezwładności względem dwóch prostopadłych osi przechodzących przez ten biegun.

K ⁼ Ix^+Iy

Promień bezwładności ciała sztywnego jest to charakterystyczny wymiar tego ciała określający w sposób syntetyczny jego kształt i rozkład masy wewnątrz tego ciała względem pewnej osi. Promień bezwładności r_b definiuje wzór

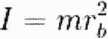
gdzie

/ - moment bezwładności ciała, m - masa.

Promień bezwładności można zdefiniować również jako odległość od osi punktu, w którym trzeba by skupić masę całego ciała, aby moment bezwładności tego punktu materialnego był równy momentowi danej bryły względem tej osi.

21.    Twierdzenie Steinera - twierdzenie mechaniki oraz wytrzymałości materiałów opisujące sposób znajdowania momentu bezwładności danej bryły względem danej osi przy danym momencie bezwładności względem osi równoległej i przechodzącej przez środek masy bryły. Jego autorem jest Jakob Steiner. Twierdzenie to można wyrazić wzorem

/ = io 4- md²

gdzie:

•    -^0- moment bezwładności względem osi przechodzącej przez środek masy,

•    /- moment bezwładności względem osi równoległej do pierwszej osi,

•    cl- odległość między osiami,

•    m - masa bryły.

Ze wzoru tego wynika, że moment bezwładności osiąga minimalną wartość, gdy oś przechodzi przez środek masy.

22.    Tarcie spoczynkowe (statyczne) - tarcie ślizgowe, występujące między dwoma ciałami gdy nie przemieszczają się względem siebie.

Siła tarcia równoważy siłę działającą na ciało. Maksymalna siła tarcia jest proporcjonalna do siły, z jaką ciało naciska na podłoże:

T = N •

gdzie T - maksymalna siła tarcia, N - nacisk, p - współczynnik tarcia statycznego zależny od materiałów, z jakich są wykonane ciała.