CCF20130109038

Na rysunku 4.12c przedstawiono wszystkie rodzaje odkształceń występujące jednocześnie.

y

A

C'

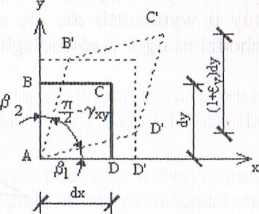
Rys. 4.12

Ze wzoru (4.9) otrzymujemy

£v=-

A dx dx

Ady

dy

(4.11)

„    du dv .    ,,    ,    .

Oznaczając przez — oraz —— intensywność przyrostu przemieszczeń u i v odek dy

powiednio w kierunku osi x, y, całkowite przyrosty długości boków możemy opisać jak następuje

Adx = — dx,    Ady =    dy .

dx    dy

Podstawienie (4.12) do (4.11) daje

du    dv

(4.12)

e_r =■

dx

^£y =

dy

(4.13)

Odkształcenie postaciowe jest wielkością bardzo małą, możemy zatem przyjąć, że kąty /3, i    są w przybliżeniu równe ich tangensom:

dv

dx

dv

P2 ~ tg^2

dx    dx ’

du

dy^ du dy    dy ’

(4.14)

gazie:

du

dy

dy - przyrost przemieszczenia u na długości odcinka dy,

dv .    .    .    „    , . ,

—— dx - przyrost przemieszczenia v na długości dx.

dx

Wobec (4.10) otrzymujemy ostatecznie

_ du dv

dy dx

(4.15)

Znając wartości e_x, e_y, y^ możemy określić odkształcenia elementów dowolnie

obróconych w stosunku do położenia elementu pierwotnego. Jeżeli po obrocie elementu prostokątnego o kąt (p otrzymamy - 0, będzie to oznaczało, że rozpatrywany element pozostanie po odkształceniu prostokątem. Odpowiadające temu

stanowi dwa wzajemnie prostopadłe wydłużenia jednostkowe £. i £ _K nazywa-

_v+-

my odkształceniami głównymi i oznaczamy przez e, i e₂ ■ Kąt nachylenia kierunków głównych wyznaczamy z zależności

tg

(4.16)

Wartości odkształceń głównych znajdujemy ze wzoru £max/. =£y =l(^£x+£y)^±-zj(£_x-£yf +Yx

'i

(4.17)

4.8. ZWIĄZKI FIZYCZNE MIĘDZY ODKSZTAŁCENIAMI I NAPRĘŻENIAMI

W zakresie odkształceń sprężystych zależność między naprężeniem i odkształceniem w pręcie rozciąganym osiowo jest liniowa (prawo Hooke’a):

a = E-e.    (4.18)

Jednocześnie pręt doznaje zwężenia określonego związkiem

£_p = —V£,    (4.19)

73