CCF20130109054

jjwuiuiLiiw    u^wac wiimiiłuiu. Zjctuwtizjiiy, z,c WlUKllil pu biruilie

wklęsłej uległy skróceniu, a po stronie wypukłej - wydłużeniu. Zatem w pręcie musi istnieć warstwa, której włókna nie uległy odkształceniu. Warstwę tę nazywamy warstwą obojętną, a jej ślad w płaszczyźnie przekroju nazywamy osią obojętną.

Zakłada się, że włókna wzdłużne nie oddziałują na siebie, wskutek czego znajdują się w jednoosiowym stanie naprężenia (proste rozciąganie i ściskanie). Zatem w przekroju normalnym pręta poddanego czystemu zginaniu występują naprężenia normalne a_x , a w przekrojach równoległych do osi nie ma naprężeń.

Warunki równowagi

Wytnijmy myślowo z belki poddanej czystemu zginaniu odcinek o długości x. Wydzielmy na polu przekroju element pola dA. Na element ten działa siła normalna dN -O_xdA. Siły zewnętrzne działające na odciętą część belki można zastąpić wektorem momentu Mg_y przyłożonym w środku ciężkości powierzchni czołowej pręta (rys. 6.25).

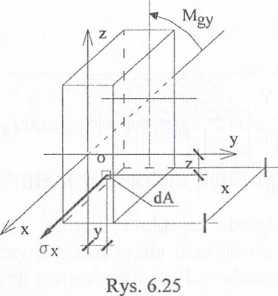
Warunki równowagi dla rozpatrywanego przypadku mają postać

(6.20)

(6.21)

^Tx = 0;    ^o_xdA = 0,

(a)

^M_y=0;    Mg_y - ja_x-zdA = 0 .

{a)

Warunek geometryczny

Rozpatrzmy odkształcenie elementu belki o długości dx (rys. 6.26).

Po wygięciu elementu przekroje końcowe obrócą się względem siebie tworząc kąt d(p. Długość odcinka 0| 0₂ nie ulegnie zmianie, gdyż należy on do warstwy obojętnej, a więc 0i 0₂ = dx. Włókno AB znajdujące się w odległości z od warstwy

uuujęinej, u pierwotnej długości dx = p dę, po odkształceniu ma długość (p + z)dę . Zatem wydłużenie jednostkowe e_x włókna Ził wynosi

e

X

(p + z)d(p - p ■ d(p _ Z P' d(p    p

(6.22)

Z powyższej zależności wynika, że odkształcenia zmieniają się liniowo, proporcjonalnie do odległości danego włókna od osi z.

M

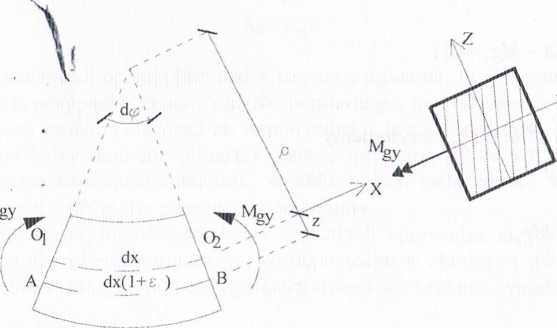
Rys. 6.26

Związki fizyczne

Zgodnie z prawem Hooke’a

^Gx ~ E -£_x ■

Wobec zależności (6.22) naprężenie normalne o_x można wyrazić jako funkcję z jak następuje

O

z

P

(6.23)

Z warunku (6.20) po uwzględnieniu (6.23) mamy

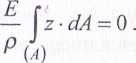
105