CCF20130109069

Odpowiedź

crf = 0,

<rf =0,125 MPa, <T,^C = 0,52 MPa, o* =1,21 MPa, of = 2,17 MPa,

<72 =-2,17 MPa, <7* =-1,21 MPa, <jf - 0,52 MPa, o 2 =-0,125 MPa,

<72=0.

PRZYKŁAD 3

Wyznaczyć naprężenia główne w punkcie K przekroju a-a belki przedstawionej na rysunku 6.56.

Dane: P = 415 kN, / = 1,5 m. Wymiary przekroju podano w mm.

!^p

—ł

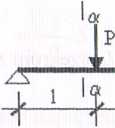
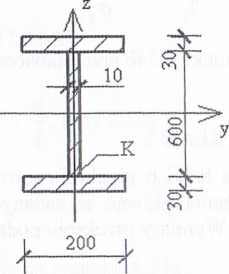
Rys. 6.56

Odpowiedź <7* =-20,8 MPa, o $ =-157 MPa.

6.4. SKRĘCANIE PRĘTÓW

Pręty stanowiące części składowe konstrukcji budowlanych mogą być obciążone układami sił, których wypadkowe działają z pewnym mimośrodem w stosunku do osi takiego elementu (rys. 6.57).

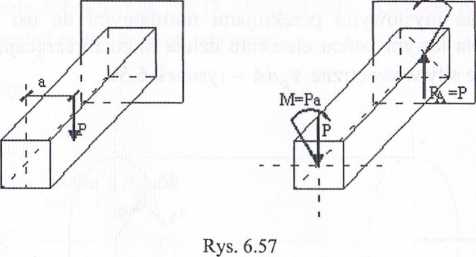
Tego rodzaju obciążenie możemy zastąpić układem równoważnym złożonyr z siły P przechodzącej przez oś pręta i pary sił o momencie M_x = Pa przyłożone w płaszczyźnie przekroju, a więc w płaszczyźnie prostopadłej do osi pręta. Siła i wywołuje wówczas zginanie pręta, moment M_x - skręcanie. Jest to przypadel wytrzymałości złożonej, który będzie omówiony w części II. Obecnie zajmujem’ się wyłącznie skręcaniem, a więc takim stanem, w którym w przekrojach po przecznych pręta występująjedynie momenty skręcające.

6.4.1. Skręcanie prętów o przekrojach kołowych

Rozpatrzmy pręt o średnicy D i długości / obciążony na końcach parami sił ze wnętrznych o momencie M(rys. 6.58).

z

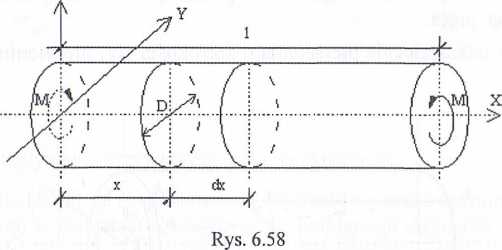
Takie obciążenie wywołuje w dowolnym przekroju pręta moment skręcający M_x = M. Zakładamy, że w każdym przekroju normalnym pręta występują naprężenia styczne T_s prostopadłe do promienia, natomiast na walcowej powierzchni wewnętrznej o dowolnym promieniu nie ma naprężeń. Zatem pręt skręcany można traktować jako zbiór koncentrycznych elementów walcowych, które nie oddziałują na siebie.

135