CCF20130109074

wych zostało opracowane przy wykorzystaniu teorii sprężystości. Ogólny sposób rozwiązania podał jako pierwszy de Saint-Venant. W dalszym ciągu zostaną podane tylko wyniki tego rozwiązania, umożliwiające przeprowadzenie obliczeń wytrzymałościowych. Dokładną analizę zagadnienia można znaleźć w podręcznikach do teorii sprężystości, jak również w cz. II skryptu „Wytrzymałość materiałów. Teoria i przykłady obliczeń”, wydanego przez PSk (autorzy: M. Bojczuk, I. Duda).

W rozważaniach dotyczących skręcania prętów niekołowych de Saint-Venant przyjął założenie, że odkształcenie przekroju pręta skręcanego składa się z dwóch części:

a)    z obrotu dookoła osi przekroju poprzecznego jako sztywnej całości; podobnie jak w przypadku skręcania pręta o przekroju kołowym,

b)    z przemieszczeń poszczególnych punktów przekroju w kierunku równoległym do osi pręta; przemieszczenia te pociągają za sobą swobodne paczenie się przekroju (tzw. deplanację).

Do obliczenia wartości naprężeń stycznych wywołanych skręcaniem pręta o przekroju prostokątnym stosuje się zależności:

_ max M x *S ~ >	(6.48)
ws
rs =TI-TS ,	(6.49)
gdzie:
Ws =ab^3.

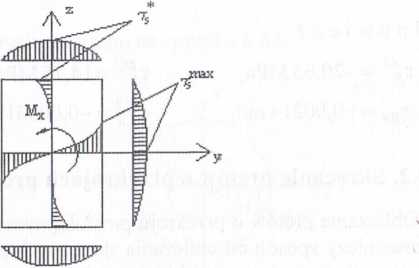
Rozkład naprężeń stycznych przedstawiono na rysunku 6.66

Rys. 6.66

Największe naprężenia styczne T™^ax występują w środkach dłuższych bokć W środkach krótszych boków naprężenia osiągają wartości . Jednostkowy 1 skręcenia znajdujemy ze wzoru

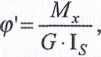
(6-

gdzie:

I s=Pb^Ą.

Wartości współczynników a,[5,ri, w zależności od stosunku — podano w tablicy

Tablici

	h Stosunek — b
	1	1,5	2	3	4	6	8	10
a	0,208	0,346	0,493	0,801	1,150	1,789	2,456	3,123
p	0,140	0,294	0,457	0,790	1,123	1,789	2,456	3,123
	1,000	0,859	0,795	0,753	0,745	0,743	0,742	0,742

PRZYKŁAD 1

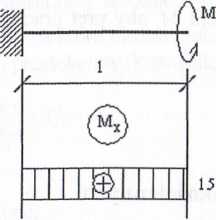
Dla pręta obciążonego jak na rysunku 6.67 dobrać wymiary przekroju p

h

przecznego, mając dane: M = 15 kNm, / = 1 m, k_s = 80 MPa oraz — = 2.

b

A z

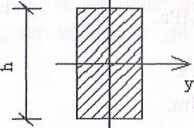
Rys. 6.67