DSC00057 (21)

/xys.20b/. Ckreślaiy jaka część energii emitowanej przez po

wierzchnię d?^ zostaje pochłonięta przez powierzchnię dPg?

Energia emitowana w kierunku skośnym z dP- wynosi

^Eoi^,dyi* ^cos c*'\    /52/

- energia emitowana w jednostce czasu przez jednoś

ci

tkę powierzchni prostopadle do powierzchni;

'f. — kąt pomiędzy normalną do powierzchni 1 a kierunkiem ku powierzchni 2.

Ila powierzchnię dP~ padnie następująca część energii

dp^. cos tf^.dPg.cos «p₂

/53/

powierzchni 2 a kierun—

e: tfp — kąt pomiędzy normalną do ki en ku powierzchni 1; r - odległość pomiędzy powierzchniami. Równanie /53/ wyraża prawo Lamberta.

Ha podstawie

Promieniowanie jednej t g' .ierzchni na drugą.

_|ego równania możemy określić wielkość energii wypromieniowa-nej we wszystkich kierunkach, jeśli znamy wielkość energii emitowanej w kierunku prostopadłym.

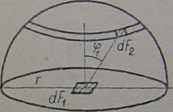
Weźmy pod uwagę pasek powierzchni leżącej na półkuli obejmującej dP^/rys.^/. Dla paska 4*2 -Powierzchnia paska wynosi

dP₂ = 2?t r.sin cpyj.r.dif^

szerokość paska = r.dxf^, długość paska = 291 r.sin

Po podstawieniu wartości dF~ w równanie /50/_t otrzymuje-

dP,

dq.sE

^.cos 9^.271 r .sintp^.d q>,.

oi

ĆE = 5§- = E , .251 ' o dF7 01

Całkując ostatnie równanie w granicach: = 0,<fy = , otrzymamy całkowitą energię wypromieniowaną we wszystkie strony

51

^Eo = \_o ^Eox •^5I'^{Bin 2 <}P₁-d‘P₁=^_oi.siń²(_fl

= 51. E

01

Ul

A więc energia wypromieniowana przez jednostkę powierzchni płaskiej ciała doskonale czarnego we wszystkich kierunkach jest 51 razy większa od energii wypromieniowanej z jednostki powierzchni, ale w kierunku prostopadłym do powierzchni.

Ponieważ

q = E_ . F

to

i =5t. E,

01

= ji-.q_x /55/

Rys.21. Promieniowanie

powierzchni w obszarze półkuli.

Ta sama zasada odnosi się i do całych promieniujących powierz -chni.

Dla ciał szarych prawa te. nie są ściśle spełnione. Okazuje się, że sprawdzają sią one przede wszystkim dla ciał o szorstkiej powierzchni w zakresie kątów 0    60°. Przy kątach

większych od 60° emisja jest mniejsza niż dla ciała doskonale czarnego. '

Wróćmy do zagadnienia wymiany ciepła pomiędzy powierzchniami ciał doskonale czarnych dP^ i dF₂ /rys.20b/. Ciepło wypromieniowane przez powierzchnię dP^ w kierunku dP₂ i po -chłonięto przez dP₂ w jednostce czasu wyraża zależność

d«Łj =

oi

dP^.cos^.dP^.cos <f₂