DSC01867 (2)

^Pp(^xp>y_p>^zp)^:

^Xp =^X0^+tp ^ax

y_P=yo+^tP^ay

Zp=Zo+t_pa_z

Wartość p parametru t wyznaczamy z równania:

A(x₀ +ta_x)+B(y₀ +ta_y) + C(z₀ +ta_z)+D = 0.

PRZYKŁADY

1. Znaleźć rzut prostej I: n:2x—3y+5z—4 = 0.

x+2

mi

2

z+l

na płaszczyznę

Rozwiązanie

Wyznaczamy płaszczyznę 7t, zawierającą prostą / i prostopadłą do płaszczyzny |. Wektor normalny płaszczyzny 7c, jest prostopadły do wektora

kierunkowego prostej / oraz do wektora n - normalnego płaszczyzny 7t.

a = [3,2,-1] - wektor kierunkowy prostej /, n = [2,-3,5] 1 wektor normalny płaszczyzny k .

Zatem

1    j k

= -7 i + 17 j+\3k,

n, = nx a =

2    -3    5

3    2-1 czyli n, =[-7,17,13] — wektor normalny płaszczyzny 1|. Punkt P₀(—2,1,-1) prostej / leży również na płaszczyźnie it,, więc płaszczyzna ta ma równanie:

7T| :-7(x + 2) + 17(y-l) + 13(z + l) = 0, czyli 7x-17^-13z + l8 = 0.

Równanie krawędziowe prostej /,, będącej rzutem prostej / na płaszczyznę n, jest postaci:

| J 2x-3y+ 5z-4 = 0 ¹ ’ [7x-17y—13z + 18=0.

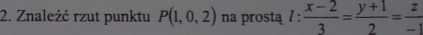
Rozwiązanie

Rzut P_x punktu P na prostą / jest punktem przebicia płaszczyzny te przechodzącej przez punkt P prostą / prostopadłą do te . Wektor kierunkowy prostej / a = [3,2, -1] jest zarazem wektorem normalnym płaszczyzny te , więc równanie tej płaszczyzny jest postaci:

3(jc-1) + 2(j/-0)-1(z-2) = 0 czyli te, :3x + 2y-z-l = 0.

Równania parametryczne danej prostej / są postaci:

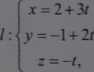
Szukany punkt P_x leży na prostej / i płaszczyźnie te, więc

3(2+3O+2(-l + 2/)-(-O-l=0

stąd

_3_

14

Punkt P_x ma więc współrzędne:

czyli

x, =2 + 3

10

7

3_ 14 1

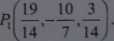
89