9576707870

Wojciech Grega, Metody Optymalizacji

xe X₀ = {*: x= Ax + Bu,x{0) = x^p,y = Cx} ue U=C„[0,T_k]

C„ [0, T_k ] - przestrzeń funkcji ciągłych [0,7*. ]. gdzie:

A =	'0 1 0 ——	, B =	' 0 ' Ks	, c=	'Cs 0'
	T L ^ls J		T L^Łs J		0 1

gdzie: xj oraz X2 są odpowiednio położeniem i prędkością kątową wału silnika,

T_s, K_SC_S są parametrami serwomechanizmu.

Funkcjonał jakości dla tego zadania zadano w postaci:

t_k

J(u) = x,(T_k )² + x₂(T_k f + ju^T< t )Ru( t )]dt 0

Dla zmierzonego stanu początkowego    (0), x₂ (0) należy znaleźć sterowanie u(t) e U,

sprowadzające stan systemu do zera, które minimalizuje funkcjonał jakości na odcinku czasu [0,7* ], a równocześnie zapewnia spełnienie: xe X₀.

Jest to zatem zadanie optymalizacji dynamicznej, z kwadratowym funkcjonałem.

Zadanie takie można zrealizować w układzie otwartym, jeśli tylko są dobrze zidentyfikowane parametry modelu napędu. Zdanie to można sprowadzić do zadania optymalizacji statycznej, tak jak pokazano to w rozdziale xxxx.

Przykład 1.7: Optymalizacja parametryczna regulatora stabilizującego

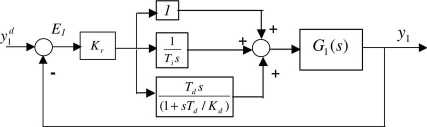
Rys. 1.11 Stabilizujące sprzężenie zwrotne z regulatorem PID

Wykład 1 -20-