9576707872

Wojciech Grega, Metody Optymalizacji

W roku 1975 John Holland na Universytecie w Michigan opublikował pracę ”Adaptation in Natural and Artifical Systems”. Praca ta, przez pewien czas zapomniana, w latach dziewięćdziesiątych została uznana za początek ewolucji podejścia do rozwiązywania problemów optymalizacji („softcomputing”).

Podsumowując rozwój tej dziedziny wiedzy można wyróżnić:

•    Okres I: Analityczne metody klasyczne, czyli metody „górskiej wspinaczki”: modele stworzone przez matematyków XVII-XIX wieku: „nieskażony” świat kwadratowych funkcji celu i wszechobecnych pochodnych. Dawały możliwości ścisłego rozwiązywania problemów „akademickich”.

•    Okres II: Oddzielenie się dziedziny „optymalizacji” i jej podział na zagadnienia szczegółowe. Rozwój obliczeń komputerowych: modyfikacje metod klasycznych oraz algorytmizacja obliczeń umożliwiały zastosowanie do praktycznych problemów nauki i techniki, w tym do funkcji nieanalitycznych.

•    Okres III: „Softcomputing”, czyli metody „odporne” na złożoność modelu procesu: algorytmy ewolucyjne, genetyczne, sieci neuronowe (rys. 1.2).

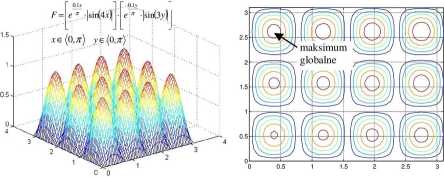
Rys. 1.2 Przykład zadania wymagającego podejścia „odpornego”

1.2 Bibliografia i inne źródła

Spis literatury jest podany na końcu niniejszego opracowania.

Zawiera on w pierwszej kolejności podręczniki akademickie, związane z materiałem zawartym w tej książce. Bogatym źródłem materiałów, w tym oprogramowania wspomagającego rozwiązywanie zadań optymalizacji, jest Internet (rys. 1.3).

Wykład 1 -4-