9576707871

Wojciech Grega, Metody Optymalizacji

• W roku 1697 Johann Bernoulli ogłosił konkurs na rozwiązanie problemu brachistochrony (gr.): „znaleźć krzywą na płaszczyźnie, łączącą dwa punkty A i B nie leżące w pionie, wzdłuż której punkt materialny poruszający się pod działaniem siły ciężkości przebywa drogę w najkrótszym czasie”. Na konkurs wpłynęło sześć prawidłowych rozwiązań od następujących matematyków i fizyków: Leibnitza, Johanna Bernoulliego, Jakub Bernoulliego, Newtona, 1’Hopitala, Tschimhausa.

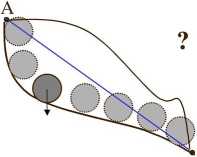
B

Rys. 1.1 Problem brachistochrony (Rozwiązanie: tuk cykloidy)

•    Początki rachunku wariacyjnego związane sa z takimi nazwiskami, jak: Lagrange (1736-1813), Hamilton (1805-1865), Weierstrass (1815-1897), Pontryagin,

•    Od roku 1939 datują się współczesne metody optymalizacji. Ich rozwój był stymulowany problemami logistyki związanymi z planowaniem wielkich operacji transportowych i desantowych w czasie II wojny światowej. Zaistniała wtedy dziedzina badań operacyjnych, a wśród, jak programowanie liniowe (Dantzig), programowanie całkowitoliczbowe (optymalny wybór spośród skończonej liczby decyzji: Cabot, Balas), i po wojnie rozwój teorii programowania nieliniowego (Kunhn,Tucker,Geoffrion),

W latach pięćdziesiątych rozwój obliczeń komputerowych spowodował wzrost zainteresowania algorytmami numerycznymi (Powell, Rosen, Fletcher), w tym także tzw. programowaniem dynamicznym, co było efektem zainteresowania procesami „z pamięcią” (Bellman, Riccati).

•    Badania kosmiczne i rywalizacja w tej dziedzinie pomiędzy USA i ZSRR stały się silną motywacją dla rozwoju metod optymalizacji. Było to związane z optymalizacją konstrukcji rakiet oraz problemami sterowania lotem w stratosferze i w przestrzeni kosmicznej. W wielu przypadkach rozwiązanie zadania optymalnego sterowania ciągiem silników, było jedynym sposobem połączenia obiektów na orbicie, przy ograniczeniach ciągu i zasobów paliwa.

•    Dążenie do optymalizacja procesów ekonomicznych, takich jak problemy alokacji produkcji, optymalny skład portfela inwestycyjnego, problemy „wielkich” (ang. large scalę) organizmów ekonomicznych stały się motywacja do rozwoju metod dekompozycji (Lasdon, Findeisen, 1970-80))

Wykład 1 -3-