DSC03725 (2)

Ze wzoru *2.344) wynika korelacja pomiędzy X i p.

określona wzorem:

(2.508)

Z uwagi na fakt. że = <pp„, wzór (2.508) przekształca się w

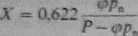
(2.509)

gdzie P oznacza ciśnienie całkowite, a 18 29 = 0,622 - stosunek mas molowych wody i powietrza, przy czym ta ostatnia masa jest wartością średnią uwzględniającą zawartość w powietrzu 21% tlenu i 79% azotu.

Ponieważ w procesie suszenia konwekcyjnego powietrze jest nośnikiem ciepła, entalpia powietrza stanowi istotny parametr w obliczeniach bilansowych. Entalpia i powietrza wilgotnego odnosi się do 1 kg powietrza bezwzględnie suchego. Jej wartość wynika ze wzoru:

(2.510)

• = Cp.r+c_p„r.Y+rX [J kg]

w którym c^, to ciepła właściwe powietrza suchego i pary wodnej, r — ciepło parowania wody, t — temperatura powietrza. Uwzględniając odpowiednie wartości liczbowe, które wynoszą:    Cp, = I kJ kg^-I K"^ł; ę_pw = 1,97 kJ-kg^-K"¹;

r = 2493 kJ, kg, można równanie (2.510) zapisać w postaci:

(2.511)

i = 2493-*10³-H l 11,97.Y)M0³ [J/kg]

2.4.15.4. Wykres Ramzina i-X

W praktyce suszarniczej obliczenia prowadzi się najczęściej metodą graficzną, wykorzystując wykres i-X. Wykres ten nazywany jest często wykresem Ramzina lub Molliera. którzy wykres en tal po wy dla powietrza wilgotnego dostosowali do potrzeb suszarnictwa. Metoda graficzna jest znacznie prostsza od metody analitycznej.

Zasady sporządzania wykresu i-X, którego wycinek pokazano na rys. 2.97, są następujące:

1)    ciśnienie barometryczne P przyjmuje się za stałe, wynoszące 993 hPa (745 mm Hgk co odpowiada średniej wieloletniej w Europie;

2)    w ukośnym układzie współrzędnych, w którym kąt między osiami wynosi 135 ', odkłada się na osi odciętych zawartość wilgoci X, na lewej osi rzędnych entalpie i oraz temperatury /, a na prawej osi rzędnych ciśnienia cząstkowe pary wodnej, p_a,

3)    pod kątem prostym do osi rzędnych nanosi się oś pomocniczą, na której znaczone są rzuty wartości X z rozwartej osi odciętych;

4) do sporządzonego w opisany sposób układu wrysowuje się: linie stałej zawartości wilgoci X — const (linie pionowe), linie stałej entalpii i — const (linie ukośne nachylone do osi rzędnych pod kątem 135°). izotermy t = const (nieco

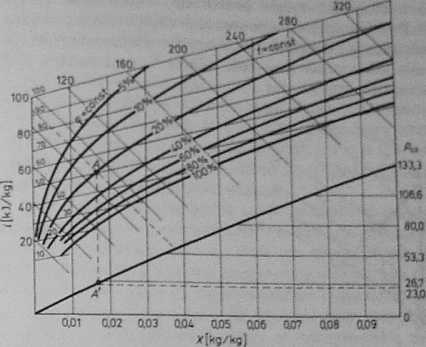
Rys. 257. Wykres hX Ramzina dla powietrza wilgotnego

nachylone do osi odciętych), linie stałej wilgotności względnej (p => const (pęk krzywych schodzących się w punkcie zera bezwzględnego);

5) prowadzi się linię stałej prężności pary wodnej.

Izotermy wykreśla się na podstawie wzoru (2.511), natomiast linie stałej wilgotności względnej na podstawie wzoru (2510). Krzywa ip = 100% (nanosi się w %) dzieli wykres na dwie części, z których tylko część górna ma znaczenie dla suszarnictwa, jako że powietrzem przesyconym suszyć się nie da.

Dogodność wykresu Ramzina wynika z faktu, że na podstawie znajomości dowolnych dwóch parametrów powietrza wilgotnego, na odpowiednich osiach można odczytać dwa pozostałe parametry. Na przykład stosunkowo łatwo mierzy się temperaturę t i wilgotność względną <p powietrza. Wartości i oraz ip wyznaczają punkt, przez który przechodzą linie dwóch pozostałych parametrów, tj. i =* const oraz X = const. Przykładem może być punkt A na rys. 297. Jeżeli z punktu tego prowadzi się w dół linię pionową, przecinającą linię stałego ciśnienia cząstkowego pary wodnej w punkcie A', to rzut punktu A' na prawą oś rzędnych wyznacza wartość p_cz dla powietrza wilgotnego. Wszystkie wielkości odczytywane z wykresu i-X odnoszą się zawsze do 1 kg powietrza absolutnie suchego zawartego w powietrzu wilgotnym.

Podczas suszenia powietrze jako czynnik suszący może ulegać ogrzaniu, ochłodzeniu i nawilżeniu. Ponadto często miesza się powietrze o różnych stanach. Wszystkie te przemiany można odnotować na wykresie Ramzina i odczytać parametry powietrza po dokonaniu każdej z ww operacji.

Ogrzewanie powietrza lub jego chłodzenie w grzejniku przeponowym nie pociąga za sobą zmiany zawartości wilgoci Przemiany te zachodzą wzdłuż hnii pionowych na wykresie i~X, czyli wzdłuż linii X * const.

189