1257951396

34

Z uwagi na fakt, że w rzeczywistych warunkach eksploatacji czas pracy elementu może być limitowany wystąpieniem dowolnego z powyższych przypadków, trwałość możemy zdefiniować jako minimalny czas spośród wyżej wymienionych t_ci

(4 6)

t_c = min {t_ci}

4.1.2. Model matematyczny procesu pełzania i zniszczenia

Równanie równowagi ciała sztywnego w układzie kartezjańskim ma postać

T311 ■

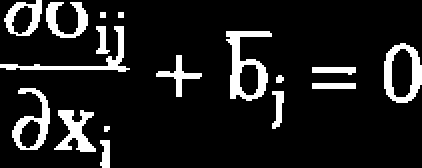
(4.7)

gdzie:

a_y — tensor naprężeń,

— siły objętościowe,

ij -1,2,3.

Tensor odkształceń e_y jest powiązany ze składowymi przemieszczeń związkiem

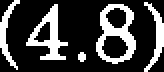
^thi, 3u, ¹

dx. ⁺ 3x_L

V    j

Analogiczny związek możemy zapisać dla prędkości odkształceń i przemieszczeń

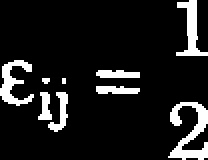
chij

3xj

3uj

3xi

(4.9)

Zakładając, że na części s_p powierzchni ciała zadano siły, a na części s_u przemieszczenia, warunki brzegowe mają postać:

Ui = Uj    na s_u

Pi=Pi    na s_D    (4.10)

Przy założeniu sumowania się odkształceń związki konstytutywne opisuje zależność:

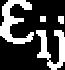
_e^E ,

“ ^eij ⁺

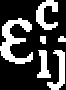
(4.11)

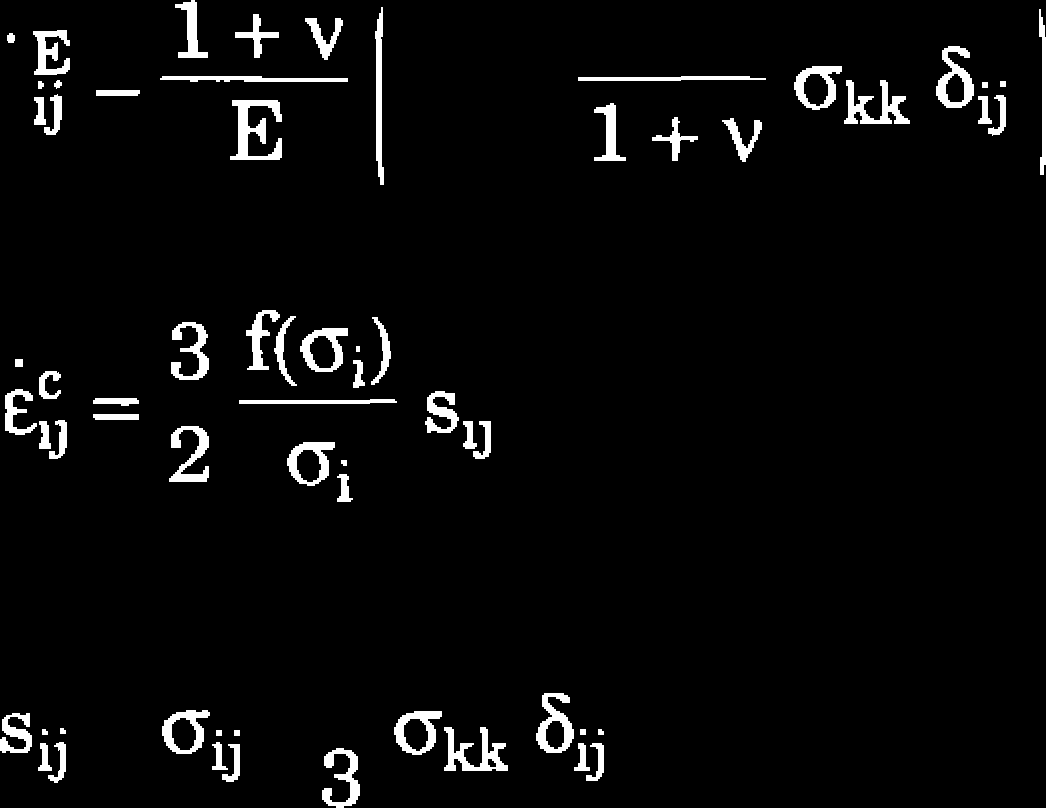
gdzie:

(4.12)

(4.13)

(4.14)

8_y - symbol Kronekera.

Przyjmując w stanie jednoosiowym opis pełzania ogólnym równaniem potęgowym

e = BaⁿK(t)    (4.15)

w stanie przestrzennym dostajemy

= | ^{B 1} K(t) (o_y - lo^ 8„)    (4.16)

w szczególności dla równania Nortona:

⁼ | B af ¹ (a_;j - ~CT_kk 5ij)    (4.17)

Przedstawiony układ równań będący modelem matematycznym procesów pełzania pozwala wyznaczyć składowe stanu naprężenia i odkształcenia w analizowanym ciele. Uwzględnienie w analizie procesów zniszczenia charakteryzowanych przez parametr zniszczenia a) wymaga uzupełnienia równań konstytutywnych o parametr co oraz równanie opisujące jego zmianę. W przypadku równania (4.17) otrzymujemy:

2 ^B (1 - co)^{n (<7ij} 3^{CkkSu)    (4}‘¹⁸⁾

Zmianę parametru zniszczenia w przestrzennym stanie naprężeń opisuje uogólnione równanie kinetyczne (3.6) [16, 18, 51]

co - A

1 - co

(4.19)