DSC07093 (6)

116

Pochodne funkcji

Rozwiązanie

aj Siła działająca na punkt materialny jat równa 0, gdy przyspieszenie tego punktu jest równe 0. Przyspieszenie punktu jest drugą pochodną jego położenia. Zatem n(t) = x*(f) = 6i— 6. Stąd a(() = 0 <=> t = 1. Punkt materialny w chwili Ł = 1 ma współrzędną * = *(!) = 4.

b) Niech z(t) $: 0 oznacza położenie ciała w chwili t ^ 0. Przyjmujemy przy tym, że x(0) = 0. Z warunków zadania mamy

_V(t) = *'(0 = *v^j.

gdzie k jat pewną stałą dodatnią. Wyznaczamy przyspieszenie a(t). Mamy

_MO=B-_(t)=Ł4o₌=^=f.

aKj^r'    ²

Z drugiej zasady dynamiki wynika, że siła działająca na ciało wyraża się wzorem

a zatem jest stała.

Pochodne funkcji wektorowych

• Przykład 4.21

a) Żuraw budowlany, którego ramię ma długość d = 20 m (rysunek), podnosi płytę z przyspieszeniem a = 0.1 m/s³. Jednocześnie dźwig obraca się wokół własnej osi z prędkość kątową u = ~ l/s. Obliczyć prędkość płyty względem

uU

otoczenia po czasie i — 5 s.

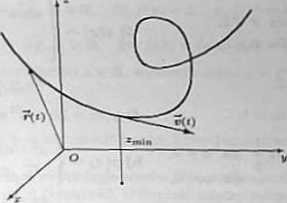
b) W chwili t samolot sportowy wykonujący akrobacje znajdował się w punkcie ⁰ wektorze wodzącym

7(t) = (z(0.vtQ.*M) = ^300coa y,300sin^,f⁵ - 20t + 20o) .

Wyznaczyć prędkość samolotu w momencie, gdy był najbliżej ziemi (płaszczyzna xOy).

s

Rozwiązanie

a) W układzie współ rzędny di wprowadzonym na rysunku położenie płyty w chwili t 2 0 jest opisane wektorem wodzącym 5(0 * (*(0t*(0»*W)» gdzie

Zatem

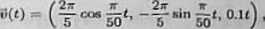
Stąd 5(5) as (1.20; 0.38; 0.50) oraz

u(6) = 15(5)| as ^(1 20j^a + (0.38)^a 5 (0.50)» = 1.35 |m/s|. b) Samolot będzie najbliżej ziemi w chwili, w której współrzędna *{t) = t⁷ - 20t + 200 = (t - 10)* + 100

będzie miała najmniejszą wartość. Z wykresu funkcji z(t) (parabola) wynika, ze tą chwilą będzie to = 10. Obliczymy prędkość samolotu w tym momencie. Mamy

3(0 = r(0 - (*'(0.»'(0.='(0) = (-60, sin y.60xco. £.21 - 2o) .

Zatem 5(f₀) = (O.COa.O).

Zadania

• Zadanie 4.1

Korzystając z definicji zbadać, czy istnieją pochodne podanych funkcji we wska-