DSCF2141 (2)

112

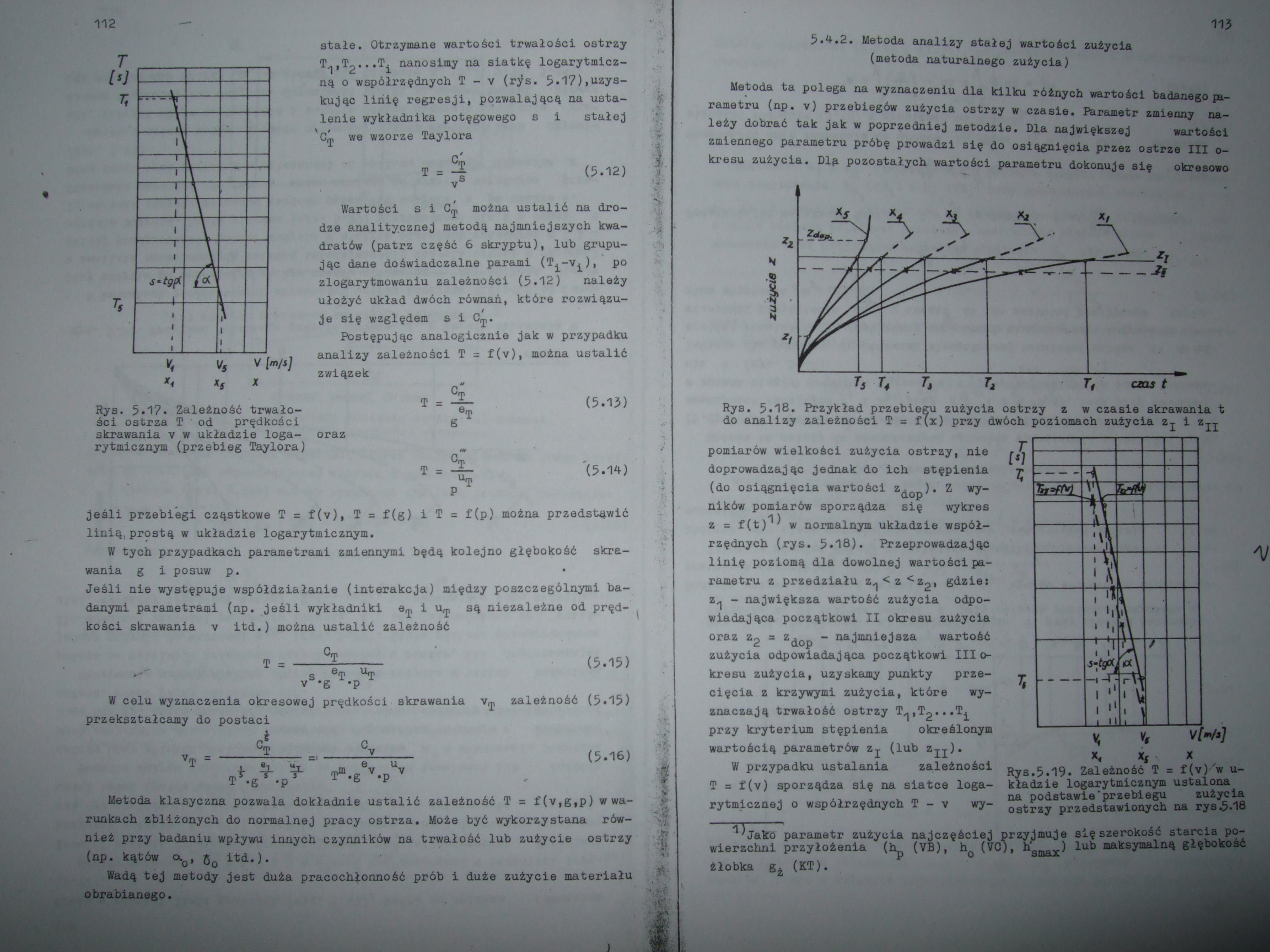
stałe. Otrzymane wartości trwałości ostrzy T^, T₂.*^Ti nanosimy na siatkę logarytmiczną o współrzędnych T - v (rys. 5»1?)iuzyskując linię regresji, pozwalającą na ustalenie wykładnika potęgowego s i stałej Cń we wzorze Taylora

li

T = 4    (5.12)

«

Rys. 5*17* Zależność trwałości ostrza !P ' od prędkości skrawania v w układzie logarytmicznym (przebieg Taylora)

v⁸

Wartości s i można ustalić na drodze analitycznej metodą najmniejszych kwadratów (patrz część 6 skryptu), lub grupując dane doświadczalne parami (T^-v^), po zlogarytmowaniu zależności (5*12) należy ułożyć układ dwóch równań, które rozwiązuje się względem s i Cj.

Postępując analogicznie Jak w przypadku analizy zależności T = f(v), można ustalić

T =

(5.13)

T =

J*T

(5.14)

Jeśli przebiegi cząstkowe T =. f(v), T = f(g) i T = f(p) można przedstawić linią, prostą w układzie logarytmicznym.

W tych przypadkach parametrami zmiennymi będą kolejno głębokość skrawania g i posuw p.    .

Jeśli nie występuje współdziałanie (interakcja) między poszczególnymi badanymi parametrami (np. Jeśli wykładniki e^ i u^, są niezależne od pręd- ^ kości skrawania v itd.) można ustalić zależność

T |

T

V *g

W celu wyznaczenia okresowej prędkości' skrawania v„, przekształcamy do postaci J

T

T

rn* ł T .g -p

e_ u„ •P

T®.g~^v—M

(5.15) zależność (5*15)

(5.16)

Metoda klasyczna pozwala dokładnie ustalić zależność T = f(v,g,p) w warunkach zbliżonych do normalnej pracy ostrza. Może być wykorzystana również przy badaniu wpływu innych czynników na trwałość lub zużycie ostrzy (np. kątów a.₀, || itd.).

Wadą tej metody Jest duża pracochłonność prób i duże zużycie materiału obrabianego.

5*4.2. Metoda analizy stałej wartości zużycia (metoda naturalnego zużycia)

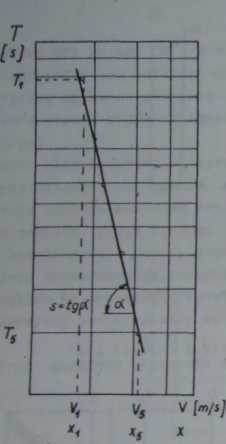
Metoda ta polega na wyznaczeniu dla kilku różnych w&rtośoi badanego jaranie tru (np. v) przebiegów zużycia ostrzy w czasie. Parametr zmienny należy dobrać tak Jak w poprzedniej metodzie. Dla największej wartości zmiennego parametru próbę prowadzi się do osiągnięcia przez ostrze III o-kresu zużycia. Dla pozostałych wartości parametru dokonuje się okresowo

Rys. 5*18. Przykład przebiegu zużycia ostrzy z w czasie skrawania t do analizy zależności I = f(x) przy dwóch poziomach zużycia z-j- i z

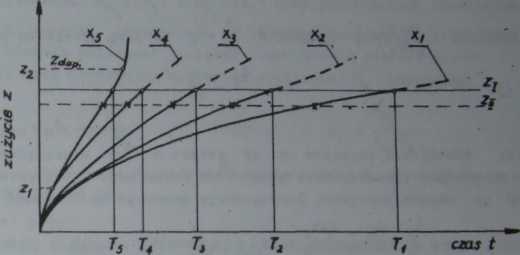
Rys.5.19* Zależność T s f(vKw u-k ładzie logarytmicznym ustalona na podstawie‘przebiegu    zużycia

ostrzy przedstawionych na rys .5*18

pomiarów wielkości zużycia ostrzy, nie doprowadzając Jednak do ich stępienia (do osiągnięcia wartości z^ ). Z wyników pomiarów sporządza się wykres

A \

z = f(t) ' w normalnym układzie współrzędnych (rys. 5*18). Przeprowadzając linię poziomą dla dowolnej wartości parametru z przedziału z^ < z ^Zg.-, gdzie: z^ - największa wartość zużycia odpowiadająca początkowi II okresu zużycia oraz Zg ^{= z}dop “ najmniejsza wartość zużycia odpowiadająca początkowi III o-kresu zużycia, uzyskamy punkty prze-oięcia z krzywymi zużycia, które wyznaczają trwałość ostrzy przy kryterium stępienia określonym wartością parametrów Zj (lub z_T-^).

W przypadku ustalania zależności T = £(v) sporządza się na siatce logarytmicznej o współrzędnych T - v wy-

TT

'Jako parametr zużycia najczęściej przyjmuje się szerokość starcia powierzchni przyłożenia (hp (VB), h_Q (vC), h^) lub maksymalną głębokość

żłobka g_ż (ED).